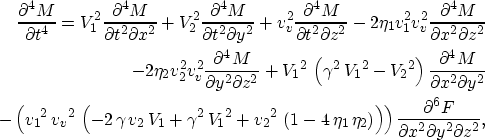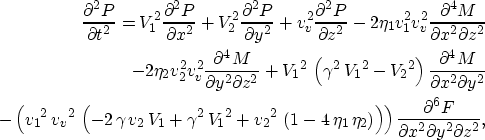Next: Analytical solutions of the
Up: Alkhalifah: Wave equation for
Previous: Accuracy tests
Using the dispersion relation of equation 17, we can derive an acoustic wave equation for
orthorhombic media as shown in Appendix A.
The resultant wave equation is sixth-order in time given by,
| 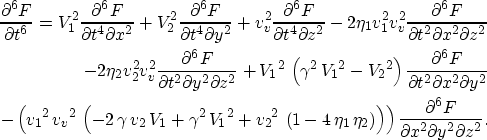 |
|
| |
| (18) |
This equation is two time-derivative orders higher than its VTI equivalent
and 4 orders higher than the conventional isotropic acoustic wave equation. Setting 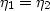 , v1=v2, and
, v1=v2, and
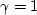 , the conditions necessary for the medium to be VTI, equation (18) reduces
to
, the conditions necessary for the medium to be VTI, equation (18) reduces
to
| 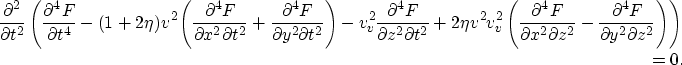 |
|
| (19) |
Substituting 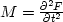 gives us the acoustic wave equation for
VTI media derived by Alkhalifah (1997a),
gives us the acoustic wave equation for
VTI media derived by Alkhalifah (1997a),
| 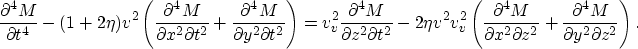 |
(20) |
Thus, as expected, equation (18) reduces to the exact VTI form when VTI model conditions
are used, and subsequently it will reduce to the exact isotropic form (the conventional second-order
acoustic wave equation) when isotropic model parameters are used (i.e., 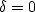 ,
, 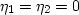 and
v1=v2=vv).
and
v1=v2=vv).
Equation (18) can be solved numerically using finite difference methods.
However, such solutions require complicated numerical evaluations based on sixth-order
approximation of derivative in time. Substituting 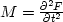 into equation (18)
yields,
into equation (18)
yields,
| 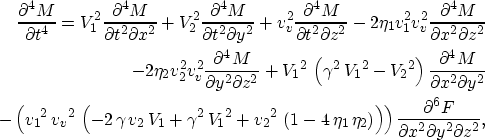 |
|
| |
| (21) |
which is a fourth order equation in derivates of t. In addition, substituting
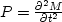 into equation (21) yields
into equation (21) yields
| 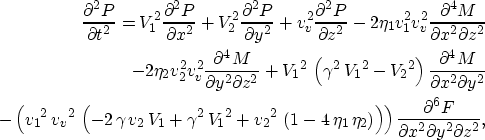 |
|
| |
| (22) |
which is now second order in derivates of t. Equation (22) also clearly displays
the various levels of parameter influence on the wave equation. For example, if 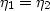 and v1=v2 the last term
in equation (22) drops.
and v1=v2 the last term
in equation (22) drops.





Next: Analytical solutions of the
Up: Alkhalifah: Wave equation for
Previous: Accuracy tests
Stanford Exploration Project
8/21/1998
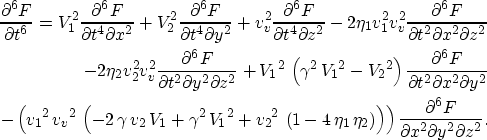
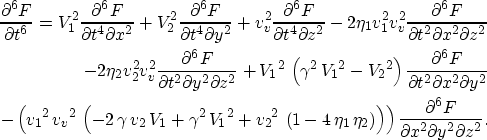
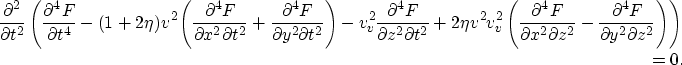
![]() into equation (18)
yields,
into equation (18)
yields,