Next: REAL DATA EXAMPLE
Up: MULTIPLE SEPARATION THEORY
Previous: Inversion
Transformation of CMP data to a space parameterized by (t,h,p)
allows the predicted primary and first water bottom related
multiple events to be represented by a simple smooth surface.
This simple representation of the primary and
multiple trends allows for a distinct separation of primary
and multiple energy.
The mask we used to separate the multiple energy from the
primary energy is a volume in the model space defined by two
surfaces; one surface follows the trend of the predicted primary events
and the other follows the trend of the predicted first water bottom
related multiple events. The predicted trends are determined for
offset and time values corresponding to each of the values
of stepout evaluated by the beam stack inversion. In order to
preserve the multiple energy alone, we retain the energy that resides at
near offsets and later times relative to the multiple trend surface,
and mute out the energy that resides at far offsets and earlier
times relative to the primary trend surface. In the region between
these two surfaces we use a linear weighting function. This weighting
function is zero at the primary surface and unity at the multiple surface.
Building a linear
weighting between the predicted primary and multiple trend
eliminates many of the effects due to truncation artifacts that would
appear if a simple step function were used to separate the
energy. Truncation artifacts are a significant problem associated
with forward modeling of beam stacked data because events in
beam stacked space have significant extent in the offset and stepout
dimensions.
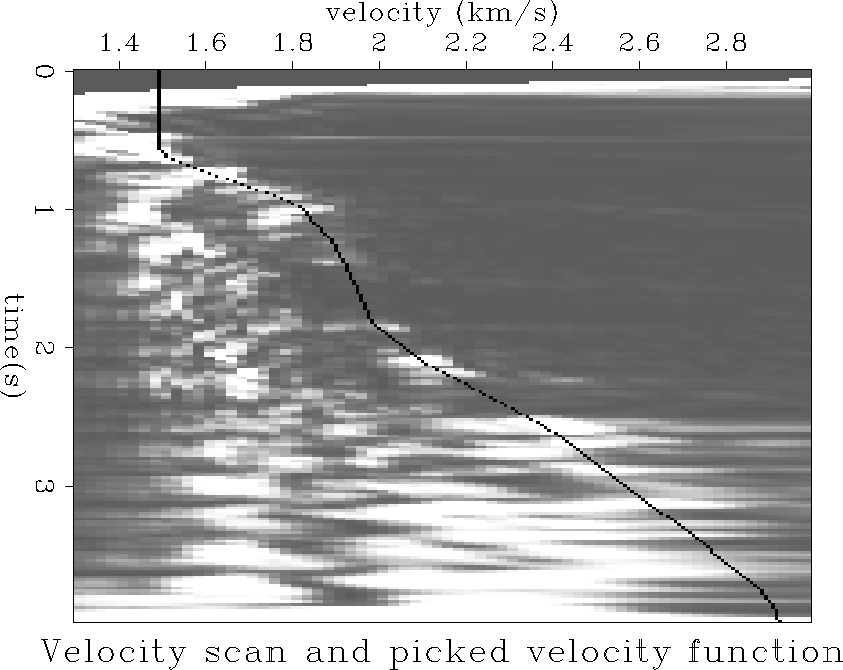
We obtained the primary velocity trend by
manually picking a velocity scan of a gather 807 of the Mobil AVO dataset
Figure 3.
velplot
Figure 3 Velocity scan of the
Mobil AVO data. The picked velocity function used in this paper is
superimposed onto the scan.
|
|  |





With the velocity trend V(t0) we predict for each stepout p:
- The expected offset of the primary trend hp(t0,p) for each value of t0.
- The two way travel time tp(t0,hp) of the primary trend
corresponding to the offset hp(t0,p).
An analyitic relation between the offset of the primary trend as a function of
t0 is often not possible, because Vp(t) is usually obtained from a
velocity scan. In order to construct the primary
surface in the (t,h,p) space, we use the relations given below for
the offset and two-way travel time of an event, and
linear interpolate between the calculated points.
| 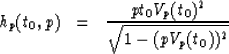 |
(8) |
| 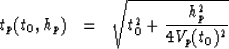 |
(9) |
The second equation is simply the Dix equation for a hyperbolic event
with velocity Vp(t0), offset hp
and the zero offset travel time t0. The first equation
is derived from Dix equation, but with the time tp being replaced
by the following equation also derived from the Dix equation:
|  |
(10) |
| (11) |
This is the two way travel time to an event parameterized by
velocity V(t0), at the stepout p and offset h of that event.
When this is substituted into the Dix equation the resulting
equation for offset is given by
equation (1). The above relations are strictly derived from the Dix
equation and thus represent the offsets and travel times of the hyperbolic
events with zero offset travel time t0 and stepout p.
We estimate the velocity trend of the
multiple energy from the RMS equation. In the following equation the primary
velocity trend is Vp(t0), the zero offset travel time to the water
bottom is tw, the travel time for each interval is 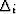 and
vw is the velocity of the water layer.
Lumley et al. (1994).
and
vw is the velocity of the water layer.
Lumley et al. (1994).
| 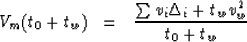 |
(12) |
A Taylor series expansion of the above equation about tw to the
second order gives:
| 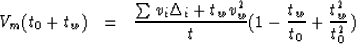 |
(13) |
| 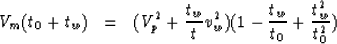 |
(14) |
Thus the expressions for the multiple trend are:
| 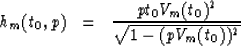 |
(15) |
| 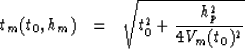 |
(16) |
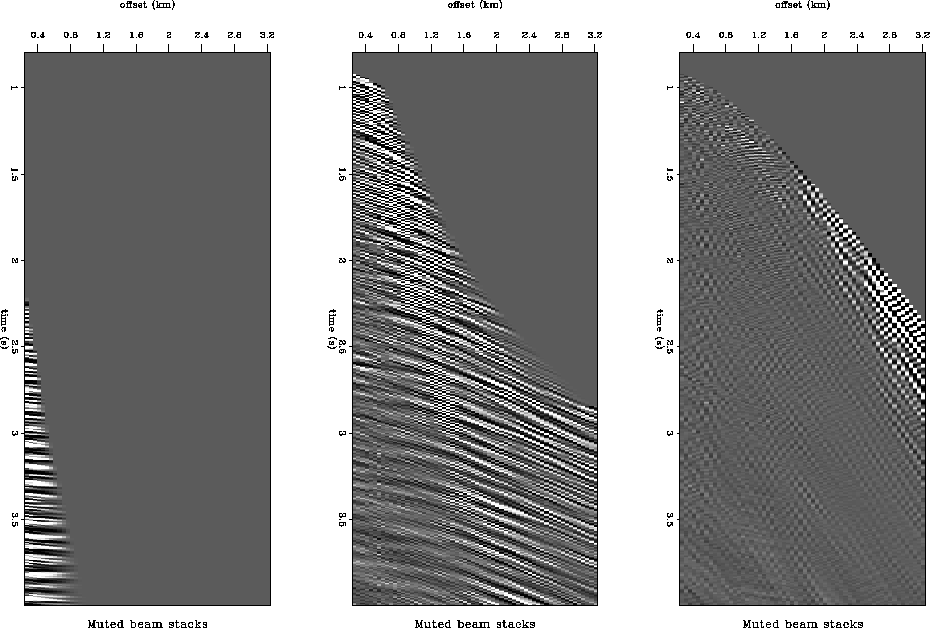
In beam stacked space the masking volume appears in each
stepout panel as an area. The
estimate of the multiple energy in beam stacked space is shown in
Figure 4. The same three slowness slices of beam stacked
space are shown in Figure 2 with out the muting applied.
cmp807m
Figure 4 Windowed multiples in
beam stacked space; left p=0.03 (s/km), middle p=0.21(s/km)
,right p=0.69(s/km)





These figures illustrate the form of the muting function for three stepout
slices of the (t,h,p) transformed cube. The energy at later times and near
offsets relative to the muting function is preserved because this is
exclusively multiple energy while the energy at earlier times and far
offsets relative to the muting function have been zeroed because this
is the region that exclusively contains primaries. The region
between the primary surface and multiple surface is a region of overlap
of the multiple and primary energy. An ideal transform to (t,h,p) space
would put no energy in this region, but the events in beam stack space
have significant extent in the
offset direction. Using the linear weighting function gives the
appropriate weight to the overlap energy in this region.
The left panel in Figure 4 corresponds to the first stepout value
inverted for, 0.03 (s/km). The separation between primary and
multiple energy in this panel is hard to discern because the
moveouts of both primary and multiple events are nearly the same near
zero offset. The second panel corresponds to a stepout value of
0.21 (s/km). In this
image the train of multiples appear as a discernible trend which
tracks linearly at an angle that lies at a stepout of about
2.67 (s/km). The primary trend has been muted out.
The final image in the trio is the panel that corresponds to a stepout
value of 0.69 (s/km). This is the velocity of the water column.
Here it can be seen that only the water
bottom energy at far offsets is stacked in while all the other
locations in the gather contribute very little, as is expected.





Next: REAL DATA EXAMPLE
Up: MULTIPLE SEPARATION THEORY
Previous: Inversion
Stanford Exploration Project
11/11/1997


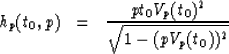

![]() and
vw is the velocity of the water layer.
Lumley et al. (1994).
and
vw is the velocity of the water layer.
Lumley et al. (1994).