Next: Inversion
Up: MULTIPLE SEPARATION THEORY
Previous: MULTIPLE SEPARATION THEORY
The beam stack operator performs the transform of data
parameterized by time and offset (t,h) to data parameterized by time,
offset and stepout (t,h,p). The generalized beam stack operator
samples each (t,h) location in the data and stacks over a localized
window of offsets, (h-l,h+l), with
a stacking trajectory function designed to evaluate the local dip
of the data. In order to evaluate the dip, the trajectory
function must have a
slope at the point (t,h) in the data equal to p. The stacking
operator is represented by:
| ![\begin{eqnarray}
CMP_{stack}(\bar{t},\bar{h},p) &=& \frac{1}{\sum_{j=-l}^{l} w(j...
...w(j\Delta{h})CMP[T_{p_{h}}(\bar{h}+j\Delta{h}),\bar{h}+j\Delta{h}]\end{eqnarray}](img1.gif) |
(1) |
where 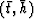 is the point in the gather being evaluated,
is the point in the gather being evaluated,
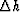 is the half offset interval,
is the half offset interval, 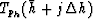 is the stacking trajectory function and
is the stacking trajectory function and 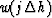 is a weighting
functionBiondi (1990).
The most elementary trajectory function is a slanting line with a dip that
corresponds to the stepout being evaluated. This is often referred to
as a local slant stack. The trajectory function in this case is
simply:
is a weighting
functionBiondi (1990).
The most elementary trajectory function is a slanting line with a dip that
corresponds to the stepout being evaluated. This is often referred to
as a local slant stack. The trajectory function in this case is
simply:
| 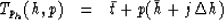 |
(2) |
The resolution of the local slant stack is limited by the
Fresnel zone of the the linear trajectory across the curved event.
We chose to use a parabolic trajectory for the local stack. The
parabolic trajectory estimates
the local curvature of the event from the offset and stepout being
evaluated Biondi (1990). This results in a larger
Fresnel zone, which translates to better resolution in the model space.
A hyperbolic function is also an option as a stacking trajectory but,
unlike the parabolic
function, the hyperbolic function is time dependent and thus more
computationally expensive to use than the parabolic or local slant
stack function. The parabolic approximation of the hyperbolic
curvature is quite good for local trajectories. The equation for the
parabolic trajectory is:
| 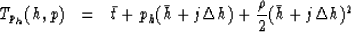 |
(3) |
where 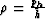 is the curvature termBiondi (1990).
The curvature term
is derived from the Dix equation and thus is based on the curvature
of hyperbolic events with the stepout p and offset h. The stepout
in equation (4) fills the role of the velocity parameter in the Dix equation.
For non-hyperbolic events
the curvature may be a misfit to the true event curvature, but for
local trajectories this misfit will be minimal. With the Dix
assumption the curvature is simply the second derivative of the Dix
equation. The Dix equation is:
is the curvature termBiondi (1990).
The curvature term
is derived from the Dix equation and thus is based on the curvature
of hyperbolic events with the stepout p and offset h. The stepout
in equation (4) fills the role of the velocity parameter in the Dix equation.
For non-hyperbolic events
the curvature may be a misfit to the true event curvature, but for
local trajectories this misfit will be minimal. With the Dix
assumption the curvature is simply the second derivative of the Dix
equation. The Dix equation is:
| 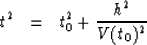 |
(4) |
The curvature is as follows:
| 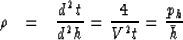 |
(5) |
A second variation on the beam stack operator we incorporated is to
allow for the length of the stacking trajectories L to vary linearly
with zero offset travel time. This increases resolution because the
Fresnel zone increases with depth as the curvature of events
becomes less.
cmp807adj
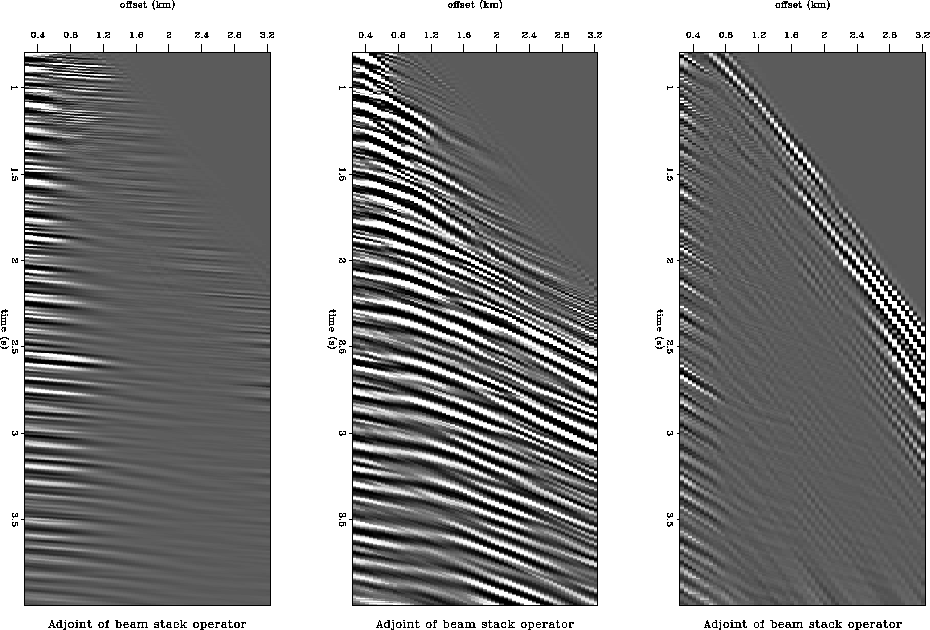
Figure 1 Three slowness slices
of the adjoint transform of the beam stacking operator applied to the
Mobil AVO gather 807; left p=0.03 (s/km), middle p=0.21(s/km)
,right p=0.69(s/km)




 cmp807bs
cmp807bs
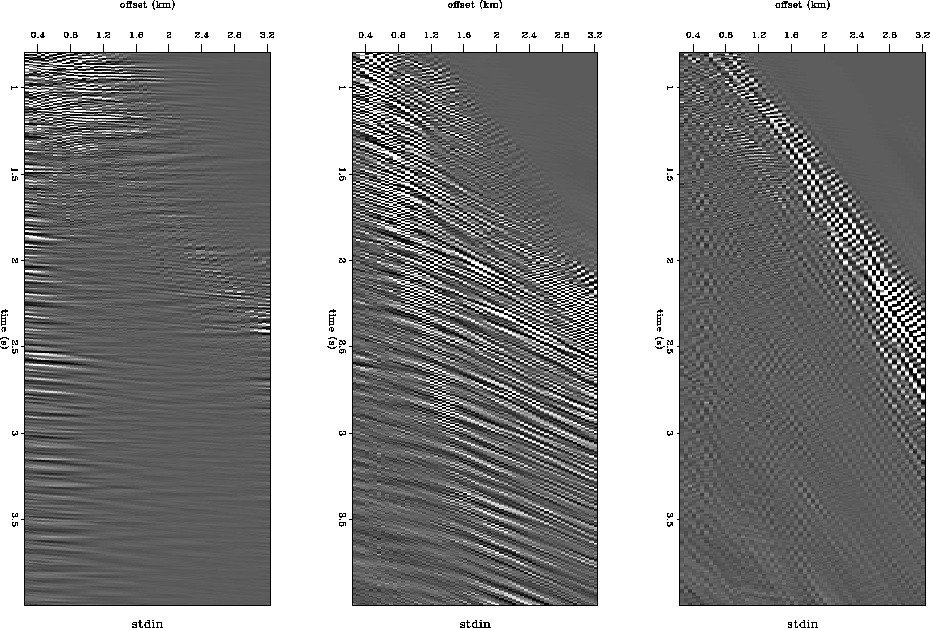
Figure 2 Three slowness slices
of the inverse transform of the beam stacking operator applied to the
Mobil AVO gather 807; left p=0.03 (s/km), middle p=0.21(s/km)
,right p=0.69(s/km)





In Figure 1 the results of the adjoint of the beam
stacking operator applied to gather 807 of the Mobil AVO data set are shown,
while in Figure 2 the results of the least squares inversion of the
beam stacking operator applied to the same Mobil gather are shown.
We will talk about the inversion in the next section.





Next: Inversion
Up: MULTIPLE SEPARATION THEORY
Previous: MULTIPLE SEPARATION THEORY
Stanford Exploration Project
11/11/1997
![\begin{eqnarray}
CMP_{stack}(\bar{t},\bar{h},p) &=& \frac{1}{\sum_{j=-l}^{l} w(j...
...w(j\Delta{h})CMP[T_{p_{h}}(\bar{h}+j\Delta{h}),\bar{h}+j\Delta{h}]\end{eqnarray}](img1.gif)
![\begin{eqnarray}
CMP_{stack}(\bar{t},\bar{h},p) &=& \frac{1}{\sum_{j=-l}^{l} w(j...
...w(j\Delta{h})CMP[T_{p_{h}}(\bar{h}+j\Delta{h}),\bar{h}+j\Delta{h}]\end{eqnarray}](img1.gif)