




Next: Masking function
Up: MULTIPLE SEPARATION THEORY
Previous: Beam stacking operator
We chose the forward operation to be the transformation from
the beam stacked space to the gather space, thus allowing for an
iterative inversion scheme to be applied to the conjugate transform of:
| 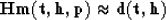 |
(6) |
where 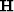 is the beam stack operator,
is the beam stack operator, 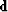 is the prestack gather
and
is the prestack gather
and 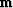 is the beam stacked space. We use a least squares estimate
of
is the beam stacked space. We use a least squares estimate
of 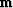 that is achieved by
minimizing the objective function with respect to the model
that is achieved by
minimizing the objective function with respect to the model
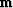 .
.
| 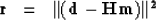 |
(7) |
where  is the residual.
A step we took to improve resolution was to reduce the
effects of the near offset data boundary. Events at data boundaries
that are not tangent to the trajectory of the beam have the undesirable
problem of not canceling out as they should, often resulting in spurious
non-physical events. This problem is especially severe at the near offsets
where large amplitude events exist.
Truncation effects are shown at the near offset of the
right panel of Figure 1, notice the corresponding
image of the inverted beam stacks do not have these artifacts.
We reduced the effects of data
boundary truncation at the near offset by estimating the data to zero
offset. We did this using a near offset interpolation scheme developed
by Jun JiJi (1994).
is the residual.
A step we took to improve resolution was to reduce the
effects of the near offset data boundary. Events at data boundaries
that are not tangent to the trajectory of the beam have the undesirable
problem of not canceling out as they should, often resulting in spurious
non-physical events. This problem is especially severe at the near offsets
where large amplitude events exist.
Truncation effects are shown at the near offset of the
right panel of Figure 1, notice the corresponding
image of the inverted beam stacks do not have these artifacts.
We reduced the effects of data
boundary truncation at the near offset by estimating the data to zero
offset. We did this using a near offset interpolation scheme developed
by Jun JiJi (1994).





Next: Masking function
Up: MULTIPLE SEPARATION THEORY
Previous: Beam stacking operator
Stanford Exploration Project
11/11/1997