Rejection of a single plane reflector volume

A field of tilted parallel planes (such as the plane reflectors discussed above) can be mathematically represented as f(x,y,z)= g(p_x x + p_y y + p_z z) where g() is an arbitrary one-dimensional function. There are various filters that destroy such a field of parallel planes. A convenient low order filter that destroys such a field is the three-component operator $(p_y \partial_z - p_z \partial_y,\ -p_x \partial_z + p_z \partial_x,\ p_x \partial_y - p_y \partial_x)$.If and only if the input data is a field of tilted parallel planes, we can find parameters p_x, p_y, p_z so that all three output volumes vanish (see the Appendix). We can solve for the correct parameters p_x, p_y, p_z by minimizing the power of the filtered data.

Instead of finite-difference operators, we decided to use related PE filters. Finite-difference representations of differential operators are susceptible to accuracy problems known in finite-difference wave propagation as ``frequency dispersion''. PE filters are not as susceptible to dispersion as finite difference operators. Furthermore, PE filters can deal with aliased dataClaerbout (1994).

A planar or 2-D PE filter  

$$\begin{array} {cc} f &a \\ g &b \\ 1 &c \\ \cdot &d \\ \cdot &e \end{array}$$ (1)

corresponds to a finite-difference operator $p_z \partial_x - p_x \partial_z$.The vertical axis is z (depth or time), the horizontal axis is x (lateral location) and the ``''s are zeros. Imagine all the coefficients vanished but d=-1 and the given 1. Such a filter would annihilate the appropriately sloping plane wave. Slopes that are not exact integers are also approximately extinguishable because the adjustable filter coefficients can interpolate in time. Filters such as (1) affect the operation $p_z \partial_x - p_x \partial_z$,which is a component of the gradient in the local set of planes, and they include a temporal deconvolution aspect and a spatial coherency aspect.

To reject an image's existing plane reflector contribution of an unknown dip, we find the filter coefficients of filter (1) that when convolved with the image yield a minimal output (residual). This set of filter coefficients is the solution of a linear inverse problem, which we solve by a conjugate gradient algorithm.

The equivalent to a three component finite difference operator $(p_y \partial_z - p_z \partial_y,\ -p_x \partial_z + p_z \partial_x,\ p_x \partial_y - p_y \partial_x)$is a combination of three planar PE filters. As Figure 2 indicates, each planar filter predicts the data in a plane vertical to any other plane. To find the three filters that reject a plane reflector volume of unknown dip, we independently solve an individual inverse problem for each filter.

 

rayab3Doper Figure 2 An East-West, a North-South, and a time-slice 2-D PE filter all applied throughout the volume. To find each filter, minimize each output power independently.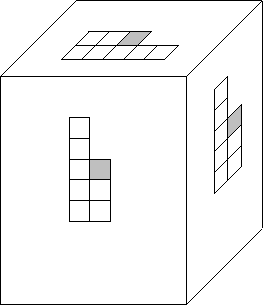

Currently, we routinely apply the planar filters on all three dimensions of the image cube, resulting in three residual volumes for each subcube. All subcubes related to a single filter direction are merged back to the original image volume, resulting in a total of three residual volumes. We have not yet found an appropriate method of combining these three outputs to a single residual volume.

The shape of a 2-D PE filter is constrained by its objective: the filter's height can be changed, but its width has to remain two columns wide. Two columns can destroy a single plane, which corresponds to our model of a single plane reflector dip within a subcube. Any additional column could destroy an additional plane and consequently could remove more energy than the single plane reflector model justifies. The length of the 2-D PE filter has to be larger than the maximal stepout (dip) of the input data. We typically choose the filter length 7, yielding a filter with 10 unknown coefficients.

By forcing a 1-D, two-term filter to predict both backward and forward, we avoid perfect predictability on growing 1-D exponentialsClaerbout (1976). To prevent predictions of exponentially growing planes, we require the 2-D PE filter to extinguish two copies of the data: the original copy and a second copy with both x and z reversed. Dips on the reversed copy are the same as on the original, but amplitude growth on one is decay on the other.

We will refer to the combined process of splitting the input image into subcubes, suppressing the local planar event in each subcube, and finally merging the subcubes to the residual image, as Lomoplan. Lomoplan has as many output cubes as the number of PE filters applied to each subcube (usually 3). Each final output cube is the size of the input volume.