MODELING REFLECTIONS

In this section, I use the results obtained from equation (18) to model P-wave reflection amplitudes numerically, from a homogeneous material representing a shale overlying another homogeneous material representing an isotropic chalk matrix with a set of vertical fractures with constant azimuth. The purpose of the modeling is to study the azimuthal behavior of P-wave reflection amplitudes as a function of fracture parameters.

The model is depicted in Figure 2. It is the same model used by Karrenbach et al. 1992. This work differs from theirs in that I directly model reflection amplitudes and compute 2-D raster plots that better show how different fracture parameters are related to the azimuthal behavior of reflection amplitudes. From these raster plots, we also obtain insight into how to derive an approximate expression for the reflection amplitudes. The two-layer model is composed of finely layered shales situated on top of a fractured chalk layer. The stiffness constants of these materials are given in Appendix A. The unfractured material stiffnesses are taken from data published by Wright 1987 and White 1982.

 

model Figure 2 A homogeneous block model. The overburden is a finely layered shale, and the underlying medium is an isotropic chalk matrix with a set of vertical fractures running parallel to the x axis.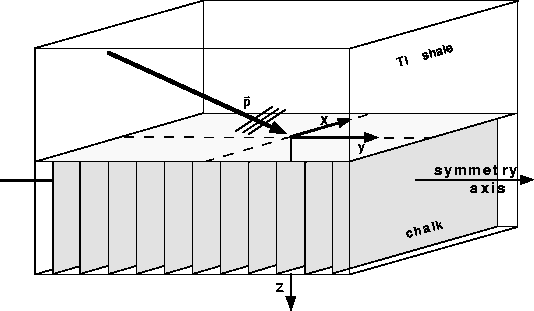

The study done on this model illustrates how different amounts of fracturing produce different azimuthal variations of the reflectivity surfaces. The isotropic chalk model is fractured using Schoenberg and Muir's 1989 group-theoretic approach (S&M), and the fracture parameters are varied using Hudson's model Hudson (1981). The model is built using Nichols's anisotropic model building library Nichols (1988), as shown in the example in Appendix B.