![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The datuming operator for a poststack data set
gathered on an irregular surface is thus
).
The datuming operator for a poststack data set
gathered on an irregular surface is thus
Now we can easily find the datuming operator
by transposing and taking the complex conjugate
of each matrix in the forward-modeling operator
shown in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The datuming operator for a poststack data set
gathered on an irregular surface is thus
).
The datuming operator for a poststack data set
gathered on an irregular surface is thus
| |
(65) |
| (66) |
| (67) |
In equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can see that the downward extrapolation
ET is preceded by the filter GT at every depth level.
We then apply the downward extrapolation operator WiT
to the wavefield that was introduced by
the operator Fi up to a given depth level.
The portion of the wavefield
that is not introduced until a given depth level
is removed by the operator Ki.
Figure
), we can see that the downward extrapolation
ET is preceded by the filter GT at every depth level.
We then apply the downward extrapolation operator WiT
to the wavefield that was introduced by
the operator Fi up to a given depth level.
The portion of the wavefield
that is not introduced until a given depth level
is removed by the operator Ki.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows this datuming operator,
while the topography is given by Figure
shows this datuming operator,
while the topography is given by Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
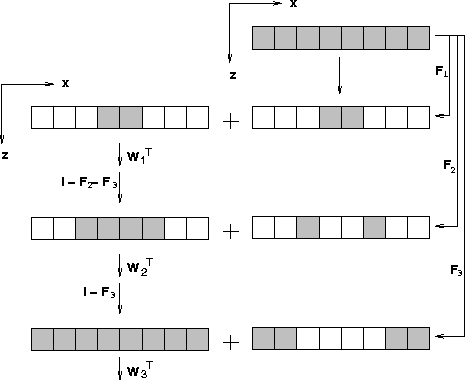 |
Coincidentally, this datuming scheme is the same as Reshef's Reshef (1991). He used the algorithm for depth migration from irregular surfaces with depth extrapolation. We can deduce that Reshef's algorithm assumes the same forward modeling algorithm as this one. By having both the forward operator and its adjoint we are prepared for inversion and velocity estimation.
|
synmdl
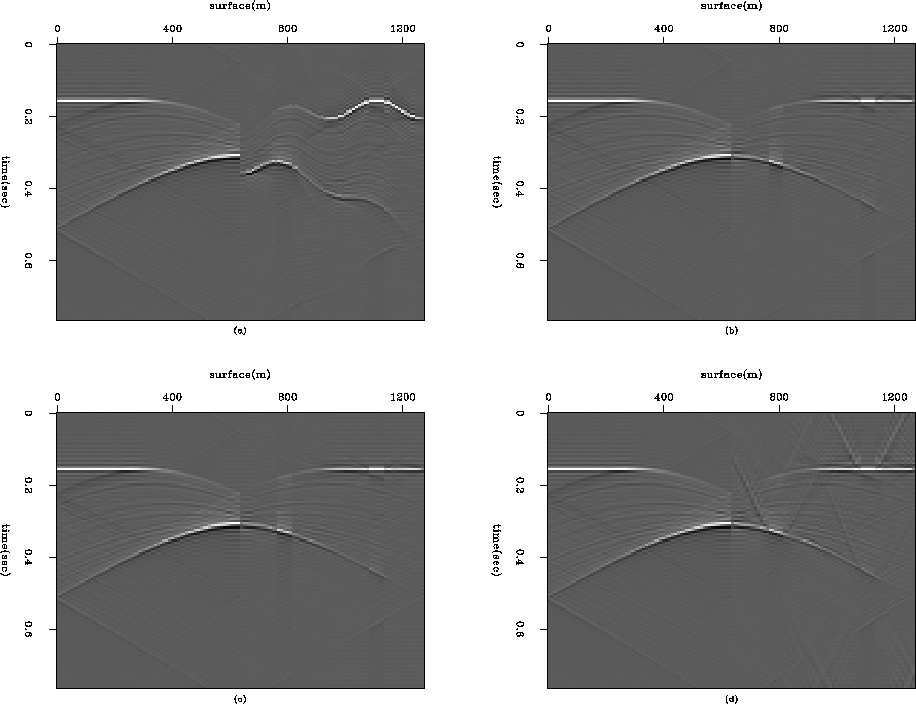
Figure 4 Synthetic model with a syncline reflector image (lower) under an undulating surface (upper). | 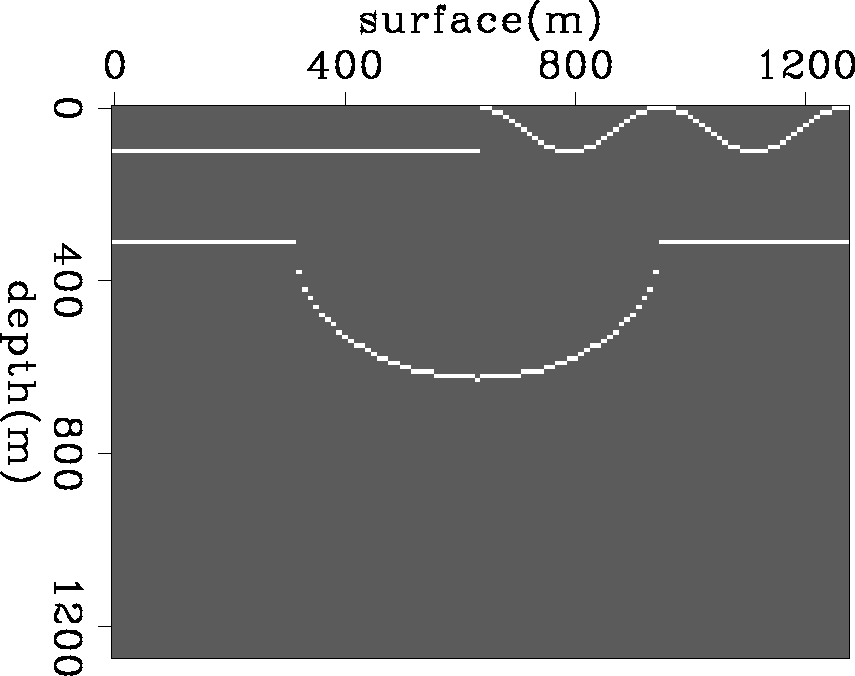 |
 |