




Next: Datuming operator
Up: Wave equation datuming
Previous: Wave equation datuming
In forward modeling,
the wavefield recorded at each geophone
along an irregular surface
is the wavefield propagated up to the depth level
where the geophones are located.
It is necessary to stop the wavefield propagation
after recording because the reflection coefficient
at the surface is almost -1.
To do so, I formulate the forward modeling operator
by propagating the wavefield upward
with a filter between extrapolation steps
to stop the wavefield propagation where it is recorded.
Then all wave fields from all depth levels
where the geophones are located
are summed together to produce the wavefield
along the irregular surface.
In order to explain the algorithm clearly and schematically,
I use a simple topography model
that has only eight geophone groups on an irregular surface,
as illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
syngeometry
Figure 1 Synthetic surface recording geometry.
Solid squares represent geophone location on an
undulating surface.
|
| 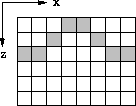 |

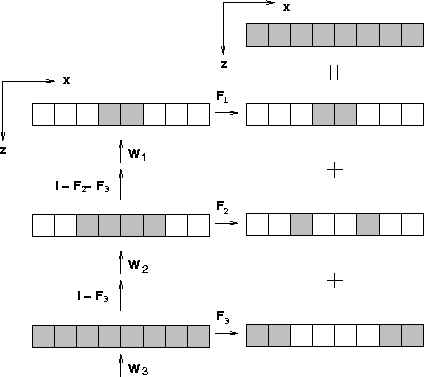
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) schematically describes
the forward modeling algorithm
for the simple model.
Wi represents upward extrapolation at the i-th depth level
and F1, F2, and F3 are spatial filters
for grabbing the wavefield where the geophones are located
at the corresponding depth levels.
The operators I-F3 and I-F2-F3 in Figure
schematically describes
the forward modeling algorithm
for the simple model.
Wi represents upward extrapolation at the i-th depth level
and F1, F2, and F3 are spatial filters
for grabbing the wavefield where the geophones are located
at the corresponding depth levels.
The operators I-F3 and I-F2-F3 in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) stop propagating the wavefield at the locations
where it is recorded below
or at the corresponding depth level
and keep propagating the wavefield at the locations
where it is not yet recorded.
Each small rectangle in Figure
stop propagating the wavefield at the locations
where it is recorded below
or at the corresponding depth level
and keep propagating the wavefield at the locations
where it is not yet recorded.
Each small rectangle in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) represents
an abstract vector that contains wave fields at the corresponding
space location.
The wavefield along the irregular surface is
obtained by summing the wave fields that are grabbed
at the various depth levels.
represents
an abstract vector that contains wave fields at the corresponding
space location.
The wavefield along the irregular surface is
obtained by summing the wave fields that are grabbed
at the various depth levels.
tpfrdschm
Figure 2 Forward modeling scheme: the schematic diagram for
forward depth extrapolation when the surface is not flat.
Wi represents the upward extrapolation operator
at the i-th depth level.
F1, F2, and F3 are spatial filters shown in the text,
and I is the identity matrix.

The forward modeling scheme
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) can be generalized algebraically,
if we divide the topography into z levels, as follows:
can be generalized algebraically,
if we divide the topography into z levels, as follows:
| ![\begin{displaymath}
\left[ \begin{array}
{c} d_0 \end{array} \right]
=
\left[ \b...
...array} \right]
\left[ \begin{array}
{c} d_z \end{array} \right]\end{displaymath}](img136.gif) |
(61) |
| ![\begin{displaymath}
E_i =
\left[ \begin{array}
{cc} I&0 \\ 0&W_i\\ \end{array} \right]\end{displaymath}](img137.gif) |
(62) |
| ![\begin{displaymath}
G_i =
\left[ \begin{array}
{cc} I&F_i\\ 0&K_i\\ \end{array} \right]\end{displaymath}](img138.gif) |
(63) |
where
| 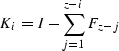 |
(64) |
In equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), d0 and dz are wave fields
on the irregular surface and the datum level, respectively.
The extrapolation operator E is followed
by the spatial filter G at every depth level.
We can see that the upward extrapolation operator Wi
is applied to the wavefield that does not
arrive at the surface because the operator Ki-1
removes the wavefield if it has arrived at any previous depth level.
All wave fields that arrive
at the surface are saved by the operator Fi-1 for the final output.
If a datum is located in the subsurface
instead of at the surface,
the operators Ki should not be used so that
the wavefield keep propagating through.
The operator Ki described in this appendix
is a crude type of transmission coefficient.
In order to implement the operator Ki more correctly,
its diagonal elements should be the transmission coefficient
according to the property of the interface and the incidence angle
of wavefield instead of 1 or .
However such a rigorous implementation of the transmission
coefficient is not practical
since it requires exhaustive ray tracing to find the incidence angle.
It is generally accepted that the transmission coefficient
is 1 on the interface between two solids and on the interface between
the solid and the air.
), d0 and dz are wave fields
on the irregular surface and the datum level, respectively.
The extrapolation operator E is followed
by the spatial filter G at every depth level.
We can see that the upward extrapolation operator Wi
is applied to the wavefield that does not
arrive at the surface because the operator Ki-1
removes the wavefield if it has arrived at any previous depth level.
All wave fields that arrive
at the surface are saved by the operator Fi-1 for the final output.
If a datum is located in the subsurface
instead of at the surface,
the operators Ki should not be used so that
the wavefield keep propagating through.
The operator Ki described in this appendix
is a crude type of transmission coefficient.
In order to implement the operator Ki more correctly,
its diagonal elements should be the transmission coefficient
according to the property of the interface and the incidence angle
of wavefield instead of 1 or .
However such a rigorous implementation of the transmission
coefficient is not practical
since it requires exhaustive ray tracing to find the incidence angle.
It is generally accepted that the transmission coefficient
is 1 on the interface between two solids and on the interface between
the solid and the air.
For the simple geometry shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
F1, F2, and F3 are simply diagonal matrices
whose elements are 1 where the geophones are located
and elsewhere.
Thus, their diagonal elements are as follows:
,
F1, F2, and F3 are simply diagonal matrices
whose elements are 1 where the geophones are located
and elsewhere.
Thus, their diagonal elements are as follows:
The operator Wi in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
can be any extrapolation scheme
including the Kirchhoff, phase-shift, split-step, or finite-difference method.
If we use the phase-shift extrapolation algorithm for Wi,
we need an additional inverse Fourier transform in every extrapolation step
because the operator G is in the space domain.
However, all the other algorithms, such as
the Kirchhoff, split-step, and finite-difference methods,
do not need any additional computation,
with the exception of the operation by G,
which is the multiplication of the extrapolated wavefield
by the zero/one filter.
)
can be any extrapolation scheme
including the Kirchhoff, phase-shift, split-step, or finite-difference method.
If we use the phase-shift extrapolation algorithm for Wi,
we need an additional inverse Fourier transform in every extrapolation step
because the operator G is in the space domain.
However, all the other algorithms, such as
the Kirchhoff, split-step, and finite-difference methods,
do not need any additional computation,
with the exception of the operation by G,
which is the multiplication of the extrapolated wavefield
by the zero/one filter.





Next: Datuming operator
Up: Wave equation datuming
Previous: Wave equation datuming
Stanford Exploration Project
2/5/2001

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) schematically describes
the forward modeling algorithm
for the simple model.
Wi represents upward extrapolation at the i-th depth level
and F1, F2, and F3 are spatial filters
for grabbing the wavefield where the geophones are located
at the corresponding depth levels.
The operators I-F3 and I-F2-F3 in Figure
schematically describes
the forward modeling algorithm
for the simple model.
Wi represents upward extrapolation at the i-th depth level
and F1, F2, and F3 are spatial filters
for grabbing the wavefield where the geophones are located
at the corresponding depth levels.
The operators I-F3 and I-F2-F3 in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) stop propagating the wavefield at the locations
where it is recorded below
or at the corresponding depth level
and keep propagating the wavefield at the locations
where it is not yet recorded.
Each small rectangle in Figure
stop propagating the wavefield at the locations
where it is recorded below
or at the corresponding depth level
and keep propagating the wavefield at the locations
where it is not yet recorded.
Each small rectangle in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) represents
an abstract vector that contains wave fields at the corresponding
space location.
The wavefield along the irregular surface is
obtained by summing the wave fields that are grabbed
at the various depth levels.
represents
an abstract vector that contains wave fields at the corresponding
space location.
The wavefield along the irregular surface is
obtained by summing the wave fields that are grabbed
at the various depth levels.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) can be generalized algebraically,
if we divide the topography into z levels, as follows:
can be generalized algebraically,
if we divide the topography into z levels, as follows:
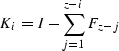
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), d0 and dz are wave fields
on the irregular surface and the datum level, respectively.
The extrapolation operator E is followed
by the spatial filter G at every depth level.
We can see that the upward extrapolation operator Wi
is applied to the wavefield that does not
arrive at the surface because the operator Ki-1
removes the wavefield if it has arrived at any previous depth level.
All wave fields that arrive
at the surface are saved by the operator Fi-1 for the final output.
If a datum is located in the subsurface
instead of at the surface,
the operators Ki should not be used so that
the wavefield keep propagating through.
The operator Ki described in this appendix
is a crude type of transmission coefficient.
In order to implement the operator Ki more correctly,
its diagonal elements should be the transmission coefficient
according to the property of the interface and the incidence angle
of wavefield instead of 1 or .
However such a rigorous implementation of the transmission
coefficient is not practical
since it requires exhaustive ray tracing to find the incidence angle.
It is generally accepted that the transmission coefficient
is 1 on the interface between two solids and on the interface between
the solid and the air.
), d0 and dz are wave fields
on the irregular surface and the datum level, respectively.
The extrapolation operator E is followed
by the spatial filter G at every depth level.
We can see that the upward extrapolation operator Wi
is applied to the wavefield that does not
arrive at the surface because the operator Ki-1
removes the wavefield if it has arrived at any previous depth level.
All wave fields that arrive
at the surface are saved by the operator Fi-1 for the final output.
If a datum is located in the subsurface
instead of at the surface,
the operators Ki should not be used so that
the wavefield keep propagating through.
The operator Ki described in this appendix
is a crude type of transmission coefficient.
In order to implement the operator Ki more correctly,
its diagonal elements should be the transmission coefficient
according to the property of the interface and the incidence angle
of wavefield instead of 1 or .
However such a rigorous implementation of the transmission
coefficient is not practical
since it requires exhaustive ray tracing to find the incidence angle.
It is generally accepted that the transmission coefficient
is 1 on the interface between two solids and on the interface between
the solid and the air.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
F1, F2, and F3 are simply diagonal matrices
whose elements are 1 where the geophones are located
and elsewhere.
Thus, their diagonal elements are as follows:
,
F1, F2, and F3 are simply diagonal matrices
whose elements are 1 where the geophones are located
and elsewhere.
Thus, their diagonal elements are as follows:
![\begin{eqnarraystar}
diag(F_1) & = & \left[ \begin{array}
{cccccccc} 0&0&0&1&1&0...
...n{array}
{cccccccc} 1&1&0&0&0&0&1&1\\ \end{array} \right] \\ \end{eqnarraystar}](img140.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
can be any extrapolation scheme
including the Kirchhoff, phase-shift, split-step, or finite-difference method.
If we use the phase-shift extrapolation algorithm for Wi,
we need an additional inverse Fourier transform in every extrapolation step
because the operator G is in the space domain.
However, all the other algorithms, such as
the Kirchhoff, split-step, and finite-difference methods,
do not need any additional computation,
with the exception of the operation by G,
which is the multiplication of the extrapolated wavefield
by the zero/one filter.
)
can be any extrapolation scheme
including the Kirchhoff, phase-shift, split-step, or finite-difference method.
If we use the phase-shift extrapolation algorithm for Wi,
we need an additional inverse Fourier transform in every extrapolation step
because the operator G is in the space domain.
However, all the other algorithms, such as
the Kirchhoff, split-step, and finite-difference methods,
do not need any additional computation,
with the exception of the operation by G,
which is the multiplication of the extrapolated wavefield
by the zero/one filter.