Next: Wave field extrapolation into
Up: The forward model
Previous: Propagation operators
The property of the angle-dependent
reflectivity matrix R(zn) in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
becomes clearer if we look at it in the Fourier domain
as de Bruin et al. (1990) does.
In order to obtain an expression for
)
becomes clearer if we look at it in the Fourier domain
as de Bruin et al. (1990) does.
In order to obtain an expression for 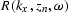 ,we start with the well-known angle-dependent reflection
coefficient
,we start with the well-known angle-dependent reflection
coefficient 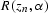 for two acoustic half-spaces separated
by an interface at zn:
for two acoustic half-spaces separated
by an interface at zn:
| 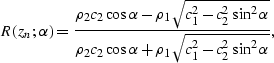 |
(44) |
where c1 and c2 are the velocities,
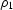 and
and 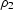 are the mass densities
of the upper and lower half-space, respectively,
and
are the mass densities
of the upper and lower half-space, respectively,
and  is the angle of incidence.
By substituting
is the angle of incidence.
By substituting 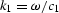 ,
, 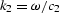 , and
, and
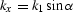 into equation (
into equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we obtain
) we obtain
| 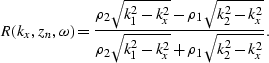 |
(45) |
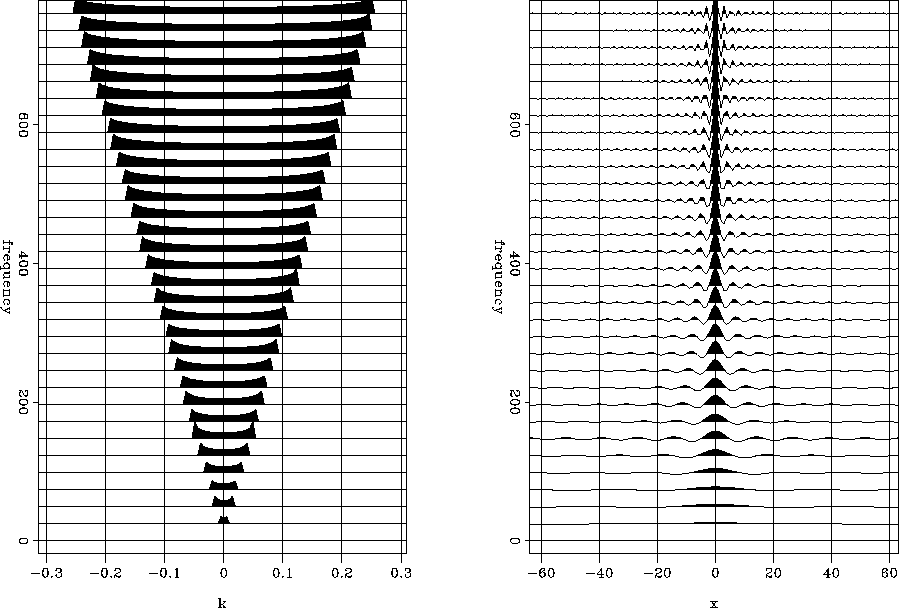
As an example, Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the angle-dependent
reflection coefficients in the
shows the angle-dependent
reflection coefficients in the 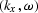 and
and
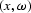 domains when c1=1500 m/s, c2=3000 m/s,
domains when c1=1500 m/s, c2=3000 m/s,
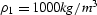 , and
, and 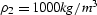 .Since the reflection is a convolution of the downgoing wave field
with the reflection coefficient,
the reflectivity matrix in equation (
.Since the reflection is a convolution of the downgoing wave field
with the reflection coefficient,
the reflectivity matrix in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
can be visualized by taking the reflection coefficient for a given
frequency in Figure
)
can be visualized by taking the reflection coefficient for a given
frequency in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and making a matrix
whose columns are down-shifted reflection coefficients of
each other.
Figure
and making a matrix
whose columns are down-shifted reflection coefficients of
each other.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows this reflectivity matrix
when
shows this reflectivity matrix
when 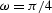 .
.
rc-wk-wx
Figure 1 Angle-dependent reflection coefficients in 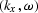 (left) and
(left) and 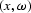 (right) domains when c1=1500 m/s, c2=3000 m/s,
(right) domains when c1=1500 m/s, c2=3000 m/s,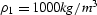 , and
, and 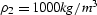 .
.





rc-mat
Figure 2 Reflectivity matrix R for 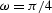 . . |
|  |










Next: Wave field extrapolation into
Up: The forward model
Previous: Propagation operators
Stanford Exploration Project
2/5/2001
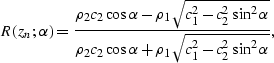
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
becomes clearer if we look at it in the Fourier domain
as de Bruin et al. (1990) does.
In order to obtain an expression for
)
becomes clearer if we look at it in the Fourier domain
as de Bruin et al. (1990) does.
In order to obtain an expression for 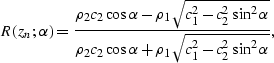
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we obtain
) we obtain
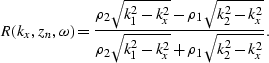
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the angle-dependent
reflection coefficients in the
shows the angle-dependent
reflection coefficients in the ![]() and
and
![]() domains when c1=1500 m/s, c2=3000 m/s,
domains when c1=1500 m/s, c2=3000 m/s,
![]() , and
, and ![]() .Since the reflection is a convolution of the downgoing wave field
with the reflection coefficient,
the reflectivity matrix in equation (
.Since the reflection is a convolution of the downgoing wave field
with the reflection coefficient,
the reflectivity matrix in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
can be visualized by taking the reflection coefficient for a given
frequency in Figure
)
can be visualized by taking the reflection coefficient for a given
frequency in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and making a matrix
whose columns are down-shifted reflection coefficients of
each other.
Figure
and making a matrix
whose columns are down-shifted reflection coefficients of
each other.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows this reflectivity matrix
when
shows this reflectivity matrix
when ![]() .
.