




Next: Examples of amplitude estimation
Up: Amplitude estimation of signal
Previous: Amplitude estimation of signal
I assume that a collection of seismic data 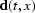 consists of signal
consists of signal 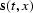 and noise
and noise 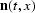 so
that
so
that
| 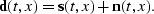 |
(99) |
The variable t corresponds to time
and x corresponds to the offset of a recorded sample
for the shot data considered
in this chapter.
For simplicity, since I assume the signal varies by
approximately t2, a scaled signal 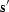 is defined as
is defined as
| 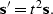 |
(100) |
so that
| 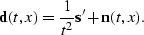 |
(101) |
The use of the t2 in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) indicates that
a sample of
) indicates that
a sample of  is multiplied by the time of that sample squared
to get the corresponding output sample in
is multiplied by the time of that sample squared
to get the corresponding output sample in 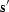 .Although the function t2 is actually a matrix with
the corresponding gain values of t2 on the diagonal,
for simplicity
I will continue to use this notation for amplitude terms that
are connected with time.
.Although the function t2 is actually a matrix with
the corresponding gain values of t2 on the diagonal,
for simplicity
I will continue to use this notation for amplitude terms that
are connected with time.
In this chapter I
assume the amplitude of the signal varies by approximately t2 and
is zero above the start time.
This amplitude variation is represented in this chapter
as the function T(t,x,v).
T(t,x,v) is not necessarily fixed as the t2 scalar,
or even fixed in x, but may be
modified to fit the data being considered. For simplicity,
I assume in this discussion that the data require a t2 scalar.
The v in T(t,x,v) represents the start time velocity.
It is unlikely that an exact amplitude representation for the signal
is needed, since I am looking only for an approximation of the
amplitude response, but the scaling for T(t,x,v) should fit the data
at least approximately.
Replacing t2 in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with
a generalized time scalar T'(t,x,v)
gives
) with
a generalized time scalar T'(t,x,v)
gives
| 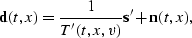 |
(102) |
where T'(t,x,v) is just T(t,x,v), except that T' produces large
values before the start time, so that 1/T'(t,x,v) is effectively
zero there.
Thus, in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
), 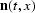 becomes
becomes 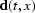 before the start time
as 1/T'(t,x,v) goes to zero.
before the start time
as 1/T'(t,x,v) goes to zero.
I further assume that the RMS amplitude
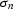 of the noise is independent
of time, while the RMS amplitude
of the noise is independent
of time, while the RMS amplitude 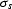 of
of 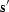 , the signal scaled by time squared, is constant.
Here,
, the signal scaled by time squared, is constant.
Here, 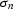 is a function of trace position, or x, making it
is a function of trace position, or x, making it
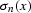 ,while
,while 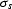 is a constant for the entire shot record.
Both
is a constant for the entire shot record.
Both 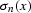 and
and 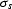 are calculated over zones of the input that
are considered typical of the noise and signal, respectively.
Each
are calculated over zones of the input that
are considered typical of the noise and signal, respectively.
Each 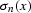 is calculated over the part of the trace before
the first arrival as
is calculated over the part of the trace before
the first arrival as
|  |
(103) |
where N is the number of samples between t=0 and x/v
is the start time for that offset,
x being the offset and v being the start time velocity.
For traces with small offsets and little data before the first breaks,
it may be possible to get a measure of 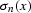 from the deeper
data, after the signal has died off.
from the deeper
data, after the signal has died off.
Next, 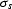 is approximated from
the shot gather using
the data after the first breaks, assuming that the reflection amplitudes
scale as t2, so
is approximated from
the shot gather using
the data after the first breaks, assuming that the reflection amplitudes
scale as t2, so
| 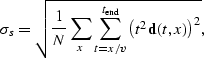 |
(104) |
where N is the total number of samples after the first break time
on all traces, and 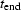 is the end of trace time.
If the mean value of each trace is zero,
is the end of trace time.
If the mean value of each trace is zero,
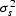 and
and 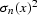 are the estimated
variances of the signal and noise.
are the estimated
variances of the signal and noise.
To make an amplitude estimation of the signal and noise,
I scale the noise and signal by the corresponding RMS amplitudes
and minimize the result,
so that
| 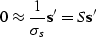 |
(105) |
and
| 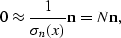 |
(106) |
where 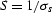 and
and 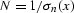 .Adding the condition that
.Adding the condition that
| 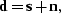 |
(107) |
or
|  |
(108) |
where 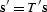 ,the regression in equation (
,the regression in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) becomes
) becomes
| 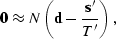 |
(109) |
making the system of regressions in equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)
| 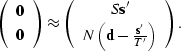 |
(110) |
Rearranging this expression produces
| 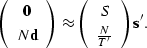 |
(111) |
Given that the least-squares solution for the expression 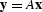 is
is
 , the least-squares solution for
, the least-squares solution for  is
is
| 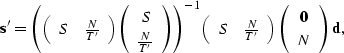 |
(112) |
which, when multiplied, gives
| 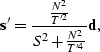 |
(113) |
or expressed as the estimated RMS amplitudes is
| 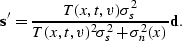 |
(114) |
The data  and signal
and signal 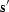 are functions of
are functions of  and t and may
be expressed as
and t and may
be expressed as 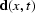 and
and 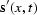 , but for the rest of
this discussion they will be expressed as simply
, but for the rest of
this discussion they will be expressed as simply  and
and 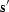 to avoid some complexity.
The original unscaled signal becomes
to avoid some complexity.
The original unscaled signal becomes
| 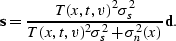 |
(115) |
The expression for the noise is
| 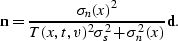 |
(116) |
It can been seen from equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
that
)
that 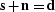 , which is consistent with equation (
, which is consistent with equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
In the present case,
S and 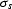 are constant over all traces,
while N(x) and
are constant over all traces,
while N(x) and 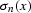 are a function of space only.
In the more general case,
these values
may be calculated from some spatial
separation of the signal and noise on the data.
are a function of space only.
In the more general case,
these values
may be calculated from some spatial
separation of the signal and noise on the data.
The scale factors in equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
only change the amplitude of the
data to what I assume would be the correct result if there existed only noise
or signal.
I have done no real separation of noise and signal other than
estimating the amplitudes. I attempt to
take the separation one step farther
in sections
)
only change the amplitude of the
data to what I assume would be the correct result if there existed only noise
or signal.
I have done no real separation of noise and signal other than
estimating the amplitudes. I attempt to
take the separation one step farther
in sections ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
and
,
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) where the spectral characteristics of the noise and signal are included.
where the spectral characteristics of the noise and signal are included.





Next: Examples of amplitude estimation
Up: Amplitude estimation of signal
Previous: Amplitude estimation of signal
Stanford Exploration Project
2/9/2001
![]() consists of signal
consists of signal ![]() and noise
and noise ![]() so
that
so
that
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) indicates that
a sample of
) indicates that
a sample of ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with
a generalized time scalar T'(t,x,v)
gives
) with
a generalized time scalar T'(t,x,v)
gives
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
), ![]() of the noise is independent
of time, while the RMS amplitude
of the noise is independent
of time, while the RMS amplitude ![]() of
of ![]() , the signal scaled by time squared, is constant.
Here,
, the signal scaled by time squared, is constant.
Here, ![]() is a function of trace position, or x, making it
is a function of trace position, or x, making it
![]() ,while
,while ![]() is a constant for the entire shot record.
Both
is a constant for the entire shot record.
Both ![]() and
and ![]() are calculated over zones of the input that
are considered typical of the noise and signal, respectively.
Each
are calculated over zones of the input that
are considered typical of the noise and signal, respectively.
Each ![]() is calculated over the part of the trace before
the first arrival as
is calculated over the part of the trace before
the first arrival as

![]() is approximated from
the shot gather using
the data after the first breaks, assuming that the reflection amplitudes
scale as t2, so
is approximated from
the shot gather using
the data after the first breaks, assuming that the reflection amplitudes
scale as t2, so
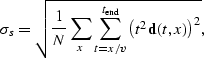
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) becomes
) becomes
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)
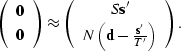
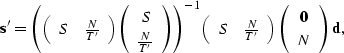
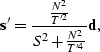
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
that
)
that ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![]() are constant over all traces,
while N(x) and
are constant over all traces,
while N(x) and ![]() are a function of space only.
In the more general case,
these values
may be calculated from some spatial
separation of the signal and noise on the data.
are a function of space only.
In the more general case,
these values
may be calculated from some spatial
separation of the signal and noise on the data.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
only change the amplitude of the
data to what I assume would be the correct result if there existed only noise
or signal.
I have done no real separation of noise and signal other than
estimating the amplitudes. I attempt to
take the separation one step farther
in sections
)
only change the amplitude of the
data to what I assume would be the correct result if there existed only noise
or signal.
I have done no real separation of noise and signal other than
estimating the amplitudes. I attempt to
take the separation one step farther
in sections ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
and
,
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) where the spectral characteristics of the noise and signal are included.
where the spectral characteristics of the noise and signal are included.