Imagine an event that is attenuated, but not removed,
by filters ![]() and
and ![]() .
.
| |
(94) |
| |
(95) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
the events included in
),
the events included in This distribution may be changed by modifying the system of equations. Consider, for example, this system:
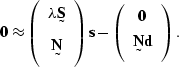 |
(96) |
Even for events that are perfectly predicted and removed by
filters ![]() and
and ![]() ,the distribution of events may be controlled by the weighting in
equation (
,the distribution of events may be controlled by the weighting in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
which is the prediction equation with the initial estimate of
the signal as the data.
In this case, the
),
which is the prediction equation with the initial estimate of
the signal as the data.
In this case, the ![]() controls the final distribution
of events in the null space of
controls the final distribution
of events in the null space of ![]() and
and ![]() .Once again,
if
.Once again,
if ![]() is less than 1,
is less than 1,
![]() will increase,
forcing relatively more of the event into the signal.
If
will increase,
forcing relatively more of the event into the signal.
If ![]() is greater than 1,
is greater than 1,
![]() will increase,
forcing relatively more of the event into the noise.
will increase,
forcing relatively more of the event into the noise.
Once again,
the weighting in system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) may be thought of in terms
of using
) may be thought of in terms
of using ![]() and
and ![]() as levelers. If
as levelers. If ![]() is weighted higher
than
is weighted higher
than ![]() , the least-squares solutions of
, the least-squares solutions of ![]() and
and ![]() will be modified
since the values of
will be modified
since the values of ![]() and
and ![]() are modified.
In the unlikely event that either
are modified.
In the unlikely event that either ![]() or
or ![]() actually becomes zero,
the weighting becomes unimportant, since one of the conditions is fit
perfectly and no better solution could be found.
In practical situations, both
actually becomes zero,
the weighting becomes unimportant, since one of the conditions is fit
perfectly and no better solution could be found.
In practical situations, both ![]() and
and ![]() will have some residual
and can only be minimized.
will have some residual
and can only be minimized.