![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is labeled
) is labeled ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
then
) is
then ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is labeled
) is labeled ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
then
) is
then
For the discussion that follows,
the calculation of the signal from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is labeled
) is labeled ![]() .
The calculation of the noise from equation (
.
The calculation of the noise from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
then
) is
then ![]() .The calculation of the noise from equation (
.The calculation of the noise from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is labeled
) is labeled ![]() .
The calculation of the signal from equation (
.
The calculation of the signal from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
then
) is
then ![]() .Is it true that
.Is it true that ![]() and is
and is ![]() ?
Ideally, yes,
but actually, the situation is more complicated.
The two signals and the two noises calculated
need not be equal, as will be shown in the examples below.
?
Ideally, yes,
but actually, the situation is more complicated.
The two signals and the two noises calculated
need not be equal, as will be shown in the examples below.
To imagine how ![]() ,consider an event that is eliminated by both filters
,consider an event that is eliminated by both filters ![]() and
and ![]() .This event is in the null space of both
.This event is in the null space of both
![]() and
and ![]() Menke (1989); Nichols (1994a); Strang (1988).
In both equation (
Menke (1989); Nichols (1994a); Strang (1988).
In both equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and equation (
) and equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
that event will be eliminated from the system,
and no information about this event will be available for the solver.
Therefore, no part of that event will occur
in the calculated solutions
)
that event will be eliminated from the system,
and no information about this event will be available for the solver.
Therefore, no part of that event will occur
in the calculated solutions ![]() and
and ![]() .The event will then be completely contained in
.The event will then be completely contained in ![]() and
and ![]() .
.
The initial estimates of ![]() and
and ![]() might be
set to values varying from zero to the data
might be
set to values varying from zero to the data ![]() when using iterative methods for solving
equations (
when using iterative methods for solving
equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
If the initial estimates of
).
If the initial estimates of ![]() and
and ![]() are zero,
the problem will appear as equations (
are zero,
the problem will appear as equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
If the initial value of the signal
).
If the initial value of the signal ![]() in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is the data
)
is the data ![]() ,the constant
,the constant
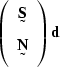 |
(90) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)
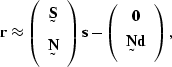 |
(91) |
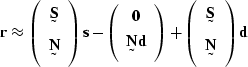 |
(92) |
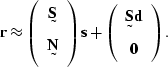 |
(93) |
When this equation is compared to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
it might be supposed that the
),
it might be supposed that the ![]() in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is
)
is ![]() from equation (
from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which was previously labeled as
), which was previously labeled as ![]() .When the initial value
.When the initial value ![]() of
of ![]() is added, the result becomes
is added, the result becomes
![]() .Instead of the previously calculated value of
.Instead of the previously calculated value of ![]() from equation (
from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
using the initial estimate of d for
),
using the initial estimate of d for ![]() in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
gives the value
)
gives the value ![]() ,
which is the same answer as equation (
,
which is the same answer as equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
A similar relationship is true for equation (
).
A similar relationship is true for equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and equation (
)
and equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) if the estimated noise
is set to
) if the estimated noise
is set to ![]() .
.
The difference between solving with zero as the initial solution
and solving with the data as the initial solution is simply where
to put the null space.
If the initial solution contains no null space data, the final solution
will not contain any of the null space data.
If the initial solution contains data that falls in the null space,
the final solution will leave this null space unchangedNichols (1994a).
The difference between equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is the placement of events that fall in the null space.
)
is the placement of events that fall in the null space.
To summarize the previous discussion,
the solutions for the signal and noise derived from
equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), (
), (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and (
), and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
are the same whether the noise or signal is calculated,
provided the initial estimates of the signal and noise are the same
and the estimates for the signal and noise sum to the data
)
are the same whether the noise or signal is calculated,
provided the initial estimates of the signal and noise are the same
and the estimates for the signal and noise sum to the data ![]() .For example, equation (
.For example, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) solved with an initial estimate of
the signal of zero assumes the noise has an initial value of the data.
Solving equation (
) solved with an initial estimate of
the signal of zero assumes the noise has an initial value of the data.
Solving equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the same initial values of the
signal being zero and the noise being the data gives the same results
for the calculated noise and data.
For a more symmetrical result, the noise and signal might both be initialized
with half the data.
This choice of initial values gives us a useful tool in specifying
how data in the null space of both
) with the same initial values of the
signal being zero and the noise being the data gives the same results
for the calculated noise and data.
For a more symmetrical result, the noise and signal might both be initialized
with half the data.
This choice of initial values gives us a useful tool in specifying
how data in the null space of both ![]() and
and ![]() are distributed.
are distributed.