When applied to data with relatively mild random noise problems, most of the cases where t-x prediction was compared to f-x prediction showed practically identical results. In tests on synthetics with simple flat or dipping events in the absence of noise, both techniques passed events without distortion. These same simple cases with an added background of relatively low-amplitude random noise also produced comparable results. The results using real data with both techniques were also similar. Differences appeared only when the signal-to-noise ratio is low.
These similarities and differences are explained by comparing the form of the t-x prediction filter and the form of the effective t-x domain filter created by f-x prediction. The individual filters calculated by the f-x prediction have the form
| |
(65) |
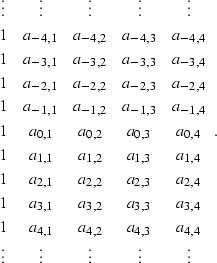 |
(66) |
 |
(67) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
but with the number of rows greatly increased.
),
but with the number of rows greatly increased.
For data with a high signal-to-noise ratio, the coefficients of the filter producing most of the prediction are expected to lie close to the center of the filter in time, since events far from the output point in time are unlikely to affect data at the output position. For data with a low signal-to-noise ratio, correlations between random events widely separated in time create undesirable lineups with significant amplitudes in the f-x prediction results. Since the f-x prediction produces a very long effective t-x filter in time, its prediction is contaminated with these random correlations, where the t-x prediction, with its smaller filter, is not. Examples showing that the f-x prediction passes more noise than the t-x prediction are presented later in this chapter for both 2-dimensional and 3-dimensional cases.
The time-length problem of the f-x prediction filter can be compared to the problem of calculating a one-dimensional prediction filter from a short time series. If a long one-dimensional prediction filter is calculated and applied to a short time series, practically everything in the time series will be predicted because of the many degrees of freedom allowed by the many filter coefficients. Having a 2-dimensional filter with a significant spatial width compensates for some of this over-prediction, but a t-x prediction filter with a short length in time is a more complete solution to the problem.
Another effect of having a long filter length in time for f-x prediction is the generation of false events. If parallel events are embedded in a background of random noise, f-x prediction generates events parallel to the original events. While both t-x and f-x techniques tend to line up noise with strong events, f-x prediction actually generates events because of its long filter length in time. These spurious events occur since parallel events in a random noise background produce an f-x filter where the prediction of one event is influenced by the presence of the other events parallel to it in spite of being widely separated in time. The t-x prediction is unaffected by the influence of widely separated events because of its short filter length in time.
An example of how f-x prediction generates spurious events
can be seen in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
In this case, two flat events are immersed in noise on the left side
of the displays, and the right side of the display is left free from noise
to show the response of the filter. In both the f-x and the t-x predictions
just one design window is used, covering all the data.
With f-x prediction, events widely spaced in time can be used to
predict an output point.
For the f-x prediction in Figure
.
In this case, two flat events are immersed in noise on the left side
of the displays, and the right side of the display is left free from noise
to show the response of the filter. In both the f-x and the t-x predictions
just one design window is used, covering all the data.
With f-x prediction, events widely spaced in time can be used to
predict an output point.
For the f-x prediction in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the noise on the
left side of the input allows the predictions to be made using
input from both events, so the equivalent t-x filter has significant
coefficients far in time from the output point.
When this filter is applied to the clean data on the right side,
spurious events generated by these widely separated coefficients
are seen.
In the f-x prediction result,
strong events are generated above and below the two
original events, and weaker events
can be seen lined up with the original events on the right side.
The t-x prediction results do not show these erroneous events.
While the f-x prediction may be modified to eliminate this problem
by constraining the filter coefficients to be smooth in frequency,
the t-x prediction did not generate spurious events since its
length in time is more naturally controlled.
, the noise on the
left side of the input allows the predictions to be made using
input from both events, so the equivalent t-x filter has significant
coefficients far in time from the output point.
When this filter is applied to the clean data on the right side,
spurious events generated by these widely separated coefficients
are seen.
In the f-x prediction result,
strong events are generated above and below the two
original events, and weaker events
can be seen lined up with the original events on the right side.
The t-x prediction results do not show these erroneous events.
While the f-x prediction may be modified to eliminate this problem
by constraining the filter coefficients to be smooth in frequency,
the t-x prediction did not generate spurious events since its
length in time is more naturally controlled.
The generation of spurious events will be considered in more
detail in the next chapter.
Although in the examples in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show that
spurious events are not generated by t-x prediction in this case,
cases where events are closely spaced allow spurious events
to be generated by both f-x and t-x prediction.
show that
spurious events are not generated by t-x prediction in this case,
cases where events are closely spaced allow spurious events
to be generated by both f-x and t-x prediction.
 |
A typical f-x prediction program has an advantage over a similar t-x prediction program because the filter length in time does not need to be specified and therefore cannot accidentally be made too short. The cost of not requiring this parameter is the risk of generating false events and of passing more noise than a t-x prediction.