Comparison of two-dimensional f-x and t-x predictions

I compared the results of varying the time-extents for t-x prediction filters in the presence of high-amplitude noise against the results of f-x prediction. In a simple noise-only case, when I used the same number of coefficients in the lateral direction for both processes, f-x prediction passed about twice the noise energy as a short time-length t-x prediction. As the time-length of the t-x prediction filter increased, the t-x prediction passed more random noise. When filters with a time-length comparable to the data time-length were used, I found almost no difference between the filters or between the results of t-x prediction and f-x prediction. Thus, because of its ability to limit the filter length in time, t-x prediction has a definite advantage over f-x prediction in removing random noise.

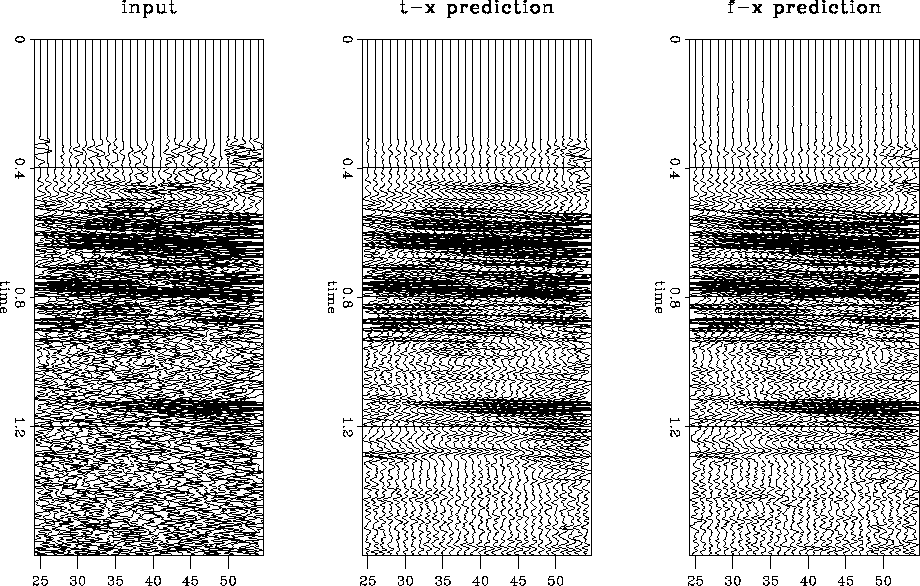
This difference in passing random noise is shown in Figure , where the results of the t-x prediction and f-x prediction are applied to a 2-dimensional stacked section. Here I used a time length of five coefficients for the t-x prediction result and a spatial length of five coefficients for both prediction methods. The window sizes in both cases were 30 traces by 300 time samples, or 0.6 seconds in this instance. This section contains a moderate amount of noise and was one of the few non-synthetic cases showing recognizable differences between t-x prediction and f-x prediction. While the results are similar, f-x prediction passes somewhat more noise than t-x prediction. The noise is most apparent in the originally zeroed area above about 0.3 seconds and in the deepest part of the section below 1.2 seconds.

 

DDw
Figure 3 2-dimensional t-x prediction and f-x prediction on a stacked line. The left section is the input; the middle section the t-x prediction result; the right section the f-x prediction result. The results of the two techniques are similar, but somewhat less noise is passed with t-x prediction than with f-x prediction.