




Next: Incorporating gain into inversion
Up: Inverse Theory for signal
Previous: Systems describing signal and
Just as the inverse filtering expressions
in frequency in ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are converted to simple scalar systems,
the expressions for the signal and noise are appealing when
expressed in the frequency or in the frequency-wavenumber domains.
The expressions for noise can be considered
scalar expressions at a constant frequency in one dimension,
and at a constant frequency and a constant wavenumber
in two-dimensions.
For example, in one dimension, equation (
are converted to simple scalar systems,
the expressions for the signal and noise are appealing when
expressed in the frequency or in the frequency-wavenumber domains.
The expressions for noise can be considered
scalar expressions at a constant frequency in one dimension,
and at a constant frequency and a constant wavenumber
in two-dimensions.
For example, in one dimension, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) becomes
) becomes
| 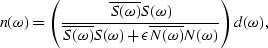 |
(55) |
where 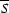 indicates the complex conjugate of S,
and all values are
scalars for a constant
indicates the complex conjugate of S,
and all values are
scalars for a constant  .For values of
.For values of  where signal is not expected,
the value of
where signal is not expected,
the value of 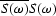 rises
and the weighting of the data into the noise increases.
For values of
rises
and the weighting of the data into the noise increases.
For values of  where signal is expected,
where signal is expected,
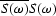 falls
and the weighting of the data into the noise decreases.
Equation (
falls
and the weighting of the data into the noise decreases.
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be recognized as an optimal or
Wiener filterPress et al. (1986).
) can be recognized as an optimal or
Wiener filterPress et al. (1986).
In the frequency-wavenumber, or  -k, domain, the same
idea applies,
except that each value of
-k, domain, the same
idea applies,
except that each value of 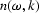 is evaluated for points
in the
is evaluated for points
in the  -k plane instead of at points of constant frequency.
The
-k plane instead of at points of constant frequency.
The  in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) becomes
) becomes
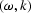 , and
the expressions are separated into samples of constant wavenumber (k)
and constant
frequency (
, and
the expressions are separated into samples of constant wavenumber (k)
and constant
frequency ( ).
This can be extended into more dimensions by specifying k1, k2, etc.,
for all the spatial directions considered.
The inversion to separate signal and noise may then be thought of
as decomposing the data into frequency and dip components,
then distributing these components between the signal and noise
as determined by the frequency and dip
components of
).
This can be extended into more dimensions by specifying k1, k2, etc.,
for all the spatial directions considered.
The inversion to separate signal and noise may then be thought of
as decomposing the data into frequency and dip components,
then distributing these components between the signal and noise
as determined by the frequency and dip
components of 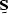 and
and 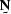 .The advantage of having more dimensions is that the noise and signal
may be better distinguished as they are spread over
.The advantage of having more dimensions is that the noise and signal
may be better distinguished as they are spread over  , k1,
k2, and so on.
Even if some overlap in the characterization of noise and signal remains,
the overlap should tend to decrease as the number of dimensions increase.
, k1,
k2, and so on.
Even if some overlap in the characterization of noise and signal remains,
the overlap should tend to decrease as the number of dimensions increase.
Although viewing the separation of signal and noise in the
frequency domains may be enlightening,
for the work done in this thesis
the inversions will generally be done in the time and space
domain which provides the advantages of simplicity of coding,
control of the filter shape,
and easy windowing of data to account for non-stationarity.





Next: Incorporating gain into inversion
Up: Inverse Theory for signal
Previous: Systems describing signal and
Stanford Exploration Project
2/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are converted to simple scalar systems,
the expressions for the signal and noise are appealing when
expressed in the frequency or in the frequency-wavenumber domains.
The expressions for noise can be considered
scalar expressions at a constant frequency in one dimension,
and at a constant frequency and a constant wavenumber
in two-dimensions.
For example, in one dimension, equation (
are converted to simple scalar systems,
the expressions for the signal and noise are appealing when
expressed in the frequency or in the frequency-wavenumber domains.
The expressions for noise can be considered
scalar expressions at a constant frequency in one dimension,
and at a constant frequency and a constant wavenumber
in two-dimensions.
For example, in one dimension, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) becomes
) becomes