




Next: Frequency-wavenumber domain expression of
Up: Inverse Theory for signal
Previous: Inverse Theory for signal
Claerbout 1995 provides
a geophysical linear inverse structure of
| 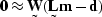 |
(43) |
| 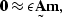 |
(44) |
where 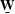 ,
, 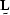 , and
, and 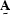 are linear operators,
are linear operators,
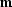 and
and  correspond to a model and to the data,
and
correspond to a model and to the data,
and  is a scale factor determining the relative weights
of these two systems.
The first regression involves how well the model fits the data.
The second regression involves limitations on what the model
is expected to be.
The matrix
is a scale factor determining the relative weights
of these two systems.
The first regression involves how well the model fits the data.
The second regression involves limitations on what the model
is expected to be.
The matrix 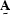 often enforces a smoothness on the model.
often enforces a smoothness on the model.
These are systems of regressions, rather than
systems of equations.
It is not expected that either 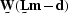 or
or 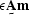 should
ever become exactly zero,
but it is expected that some minimum of these expressions can be found
by adjusting the model
should
ever become exactly zero,
but it is expected that some minimum of these expressions can be found
by adjusting the model 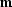 .Alternatively,
the regressions in (
.Alternatively,
the regressions in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be expressed as
the system of equations
) can be expressed as
the system of equations
| 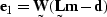 |
(45) |
| 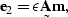 |
(46) |
where 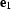 and
and 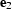 are to be minimized.
are to be minimized.
Paralleling the arguments in Claerbout 1995,
if 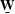 is replaced with a filtering operator
is replaced with a filtering operator 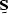 that annihilates
any signal s on which it operates so that
that annihilates
any signal s on which it operates so that 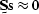 ,
,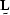 is replaced by the identity matrix
is replaced by the identity matrix 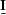 ,
,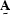 is replaced by a filtering operator
is replaced by a filtering operator 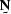 that annihilates
any noise
that annihilates
any noise  on which it operates, so that
on which it operates, so that 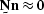 ,and
,and 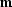 is replaced with the noise
is replaced with the noise  that is to be calculated and
removed from the data
that is to be calculated and
removed from the data  ,equations (
,equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) become
) become
| 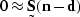 |
(47) |
| 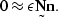 |
(48) |
An alternative method
of getting equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) would be
to start from the definitions of the signal annihilation filter and
the noise annihilation filter:
) would be
to start from the definitions of the signal annihilation filter and
the noise annihilation filter:
| 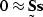 |
(49) |
| 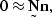 |
(50) |
that is, the signal annihilation filter 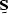 applied to the signal
applied to the signal  produces something that is almost zero, and
the noise annihilation filter
produces something that is almost zero, and
the noise annihilation filter 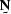 applied to the noise
applied to the noise  produces something that is almost zero.
Since the data
produces something that is almost zero.
Since the data  is defined as the sum of the signal
is defined as the sum of the signal  and the noise
and the noise  ,that is,
,that is, 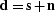 ,
,  in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) may be replaced with
) may be replaced with 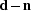 .Making this substitution and allowing for a scale factor
.Making this substitution and allowing for a scale factor  once more
gives equations (
once more
gives equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
Combining the systems
shown in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into a single system gives
) into a single system gives
| 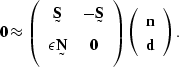 |
(51) |
Moving the expressions that depend on the data to the left-hand side
and keeping those that depend on the unknown noise on the right-hand side
gives
| 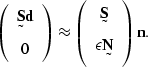 |
(52) |
This system may be solved by either minimizing the error
as in Claerbout 1995 or by substituting directly into
the solution for the normal equations.
In either case the solution for  is
is
| 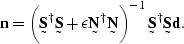 |
(53) |
Once again,  indicates the conjugate-transpose, or adjoint,
which is simply the transpose when all values are real.
indicates the conjugate-transpose, or adjoint,
which is simply the transpose when all values are real.
Since the signal  may be expressed as
may be expressed as 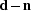 ,the solution for the signal is
,the solution for the signal is
| 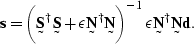 |
(54) |





Next: Frequency-wavenumber domain expression of
Up: Inverse Theory for signal
Previous: Inverse Theory for signal
Stanford Exploration Project
2/9/2001
![]() or
or ![]() should
ever become exactly zero,
but it is expected that some minimum of these expressions can be found
by adjusting the model
should
ever become exactly zero,
but it is expected that some minimum of these expressions can be found
by adjusting the model ![]() .Alternatively,
the regressions in (
.Alternatively,
the regressions in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be expressed as
the system of equations
) can be expressed as
the system of equations
![]() is replaced with a filtering operator
is replaced with a filtering operator ![]() that annihilates
any signal s on which it operates so that
that annihilates
any signal s on which it operates so that ![]() ,
,![]() is replaced by the identity matrix
is replaced by the identity matrix ![]() ,
,![]() is replaced by a filtering operator
is replaced by a filtering operator ![]() that annihilates
any noise
that annihilates
any noise ![]() on which it operates, so that
on which it operates, so that ![]() ,and
,and ![]() is replaced with the noise
is replaced with the noise ![]() that is to be calculated and
removed from the data
that is to be calculated and
removed from the data ![]() ,equations (
,equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) become
) become
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) would be
to start from the definitions of the signal annihilation filter and
the noise annihilation filter:
) would be
to start from the definitions of the signal annihilation filter and
the noise annihilation filter:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) may be replaced with
) may be replaced with ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into a single system gives
) into a single system gives
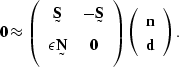
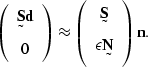
![]() is
is
![]() may be expressed as
may be expressed as ![]() ,the solution for the signal is
,the solution for the signal is