Next: Improving the signal-prediction filter
Up: Random noise removal enhanced
Previous: Shortcomings of prediction filtering
As described in chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
a structure for creating an inverse may be
,
a structure for creating an inverse may be
| 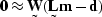 |
(76) |
| 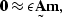 |
(77) |
where 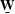 ,
, 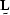 , and
, and 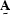 are linear operators,
and
are linear operators,
and 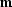 and
and  correspond to a model and to the data.
The value of
correspond to a model and to the data.
The value of  is used to weight the relative importance
of (
is used to weight the relative importance
of (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Replacing
).
Replacing 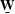 with the signal annihilation filter
with the signal annihilation filter 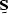 ,
,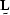 with
with 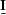 , the identity matrix, and ignoring
, the identity matrix, and ignoring
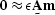 for the moment gives
an expression
for the moment gives
an expression 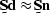 for calculating the noise from
the data given the signal annihilation filter
for calculating the noise from
the data given the signal annihilation filter 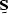 .The expression
.The expression 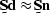 is not useful in itself for calculating the noise
is not useful in itself for calculating the noise  ,since the filter
,since the filter 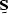 is not perfect and
is unlikely to completely annihilate the
signal to the point where the inversion for
is not perfect and
is unlikely to completely annihilate the
signal to the point where the inversion for  could not restore it.
Without additional constraints,
the obvious solution to
could not restore it.
Without additional constraints,
the obvious solution to 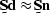 is
is 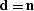 .In practice, I have found that,
although the filter
.In practice, I have found that,
although the filter 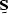 could attenuate the signal significantly,
a simple inversion of
could attenuate the signal significantly,
a simple inversion of
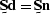 for
for  restores much of the signal
into the calculated noise
restores much of the signal
into the calculated noise  .What is needed is a constraint to replace
.What is needed is a constraint to replace 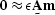 in system (
in system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
The constraint used here to keep signal out of the calculated noise
is that the noise is approximately
the noise estimated from prediction filtering 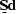 .This is a reasonable approximation, since
.This is a reasonable approximation, since
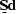 should be somewhat close to the actual noise.
The difference between the actual noise
should be somewhat close to the actual noise.
The difference between the actual noise  and the approximated noise
and the approximated noise 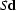 should be fairly small and involves only the response of
the noise to the filter
should be fairly small and involves only the response of
the noise to the filter 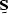 .The approximation is weighted as
.The approximation is weighted as 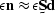 .The value for
.The value for  may be changed to account for the signal-to-noise
ratio of the data.
may be changed to account for the signal-to-noise
ratio of the data.
The system of regressions to be solved
is now
| 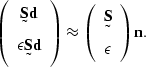 |
(78) |
The results of solving this system are referred to
as inversion prediction in the following discussion to distinguish
it from prediction filtering.
Since this system estimates  from the approximation
from the approximation 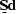 ,it is reasonable to initialize
,it is reasonable to initialize  to
to 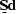 before entering
the iterative solver.
Another reason for initializing
before entering
the iterative solver.
Another reason for initializing  to
to 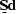 is that
the filter
is that
the filter 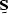 is generally small and will pass only a
limited range of spatial and temporal frequencies.
In the case of a spike in the data,
inversion for the noise with a small filter does not allow the complete
restoration of the spike.
Because the noise is expected to be almost white
and in some cases dominated by spikes,
initializing
is generally small and will pass only a
limited range of spatial and temporal frequencies.
In the case of a spike in the data,
inversion for the noise with a small filter does not allow the complete
restoration of the spike.
Because the noise is expected to be almost white
and in some cases dominated by spikes,
initializing  to
to 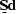 improves the calculation of
improves the calculation of
 and reduces the number of iterations needed.
and reduces the number of iterations needed.
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) expressed as a minimization of
the residual
) expressed as a minimization of
the residual  is
is
| 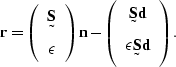 |
(79) |
Initializing  to
to 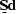 involves adding
involves adding
| 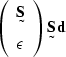 |
(80) |
to the right-hand side
of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to produce, with some simplification,
) to produce, with some simplification,
| 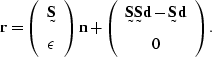 |
(81) |
Since the iterative solver just updates  without regard
to the initial value Claerbout (1995),
the value of
without regard
to the initial value Claerbout (1995),
the value of  in this equation may be considered as the change
of the calculated noise from the first estimate of the noise
in this equation may be considered as the change
of the calculated noise from the first estimate of the noise 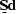 .This may be expressed as
.This may be expressed as
| 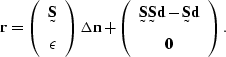 |
(82) |
This is the effective system of regressions that is implimented
in this chapter.
The results of inversion prediction are sensitive to the value of  .At the moment, the optimum value of
.At the moment, the optimum value of  is uncertain.
It would seem that
is uncertain.
It would seem that  should decrease as the signal-to-noise
ratio decreases, since the difference between the actual noise
should decrease as the signal-to-noise
ratio decreases, since the difference between the actual noise  and the estimated noise
and the estimated noise 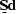 is larger.
However, in the presence of strong noise,
the larger
is larger.
However, in the presence of strong noise,
the larger  is, the more stable the inversion should be.
If
is, the more stable the inversion should be.
If  is relatively large, around 1.0,
the amplitudes of the reflections are preserved and spurious events
are somewhat suppressed.
As
is relatively large, around 1.0,
the amplitudes of the reflections are preserved and spurious events
are somewhat suppressed.
As  gets very large, the result approaches the prediction
filter result.
When
gets very large, the result approaches the prediction
filter result.
When  gets small, the amplitudes of the reflectors are
attenuated, since the signal filter
gets small, the amplitudes of the reflectors are
attenuated, since the signal filter 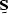 does not perfectly annihilate
the signal before the inversion.
For small
does not perfectly annihilate
the signal before the inversion.
For small  , the spurious events tend to return also.
The best value of
, the spurious events tend to return also.
The best value of  appears to be different for samples with Gaussian noise than
for samples with uniformly distributed noise.
For most work, it appears that good values of
appears to be different for samples with Gaussian noise than
for samples with uniformly distributed noise.
For most work, it appears that good values of  vary
from 0.1 to 3.0.
Small values of
vary
from 0.1 to 3.0.
Small values of  remove background noise, but seem
to introduce organized noise into the calculated signal.
For the real data examined,
the background noise increases as
remove background noise, but seem
to introduce organized noise into the calculated signal.
For the real data examined,
the background noise increases as  increases,
and the continuity of the data increases as
increases,
and the continuity of the data increases as  decreases.
Further work is needed to determine how the strength and type
of noise affects the value of
decreases.
Further work is needed to determine how the strength and type
of noise affects the value of  .
.
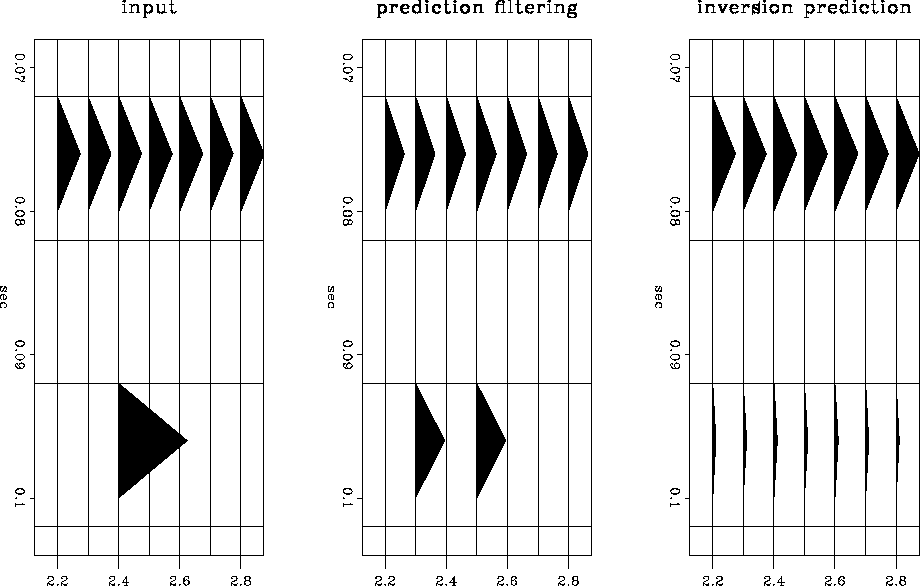
An example of the difference between prediction filtering and
inversion prediction is seen in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The filter
.
The filter 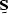 is calculated from the data to predict the flat event.
When
is calculated from the data to predict the flat event.
When 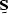 is applied to the spike, the filter response can be seen
in the prediction-filter result.
The inversion prediction result has effectively eliminated the filter response.
is applied to the spike, the filter response can be seen
in the prediction-filter result.
The inversion prediction result has effectively eliminated the filter response.
onespikea
Figure 2
A comparison of the action of a t-x prediction filter and an
inversion prediction on a spike.










Next: Improving the signal-prediction filter
Up: Random noise removal enhanced
Previous: Shortcomings of prediction filtering
Stanford Exploration Project
2/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
a structure for creating an inverse may be
,
a structure for creating an inverse may be
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
a structure for creating an inverse may be
,
a structure for creating an inverse may be
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
Replacing
).
Replacing ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![]() .This is a reasonable approximation, since
.This is a reasonable approximation, since
![]() should be somewhat close to the actual noise.
The difference between the actual noise
should be somewhat close to the actual noise.
The difference between the actual noise ![]() and the approximated noise
and the approximated noise ![]() should be fairly small and involves only the response of
the noise to the filter
should be fairly small and involves only the response of
the noise to the filter ![]() .The approximation is weighted as
.The approximation is weighted as ![]() .The value for
.The value for ![]() may be changed to account for the signal-to-noise
ratio of the data.
may be changed to account for the signal-to-noise
ratio of the data.
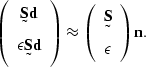
![]() from the approximation
from the approximation ![]() ,it is reasonable to initialize
,it is reasonable to initialize ![]() to
to ![]() before entering
the iterative solver.
Another reason for initializing
before entering
the iterative solver.
Another reason for initializing ![]() to
to ![]() is that
the filter
is that
the filter ![]() is generally small and will pass only a
limited range of spatial and temporal frequencies.
In the case of a spike in the data,
inversion for the noise with a small filter does not allow the complete
restoration of the spike.
Because the noise is expected to be almost white
and in some cases dominated by spikes,
initializing
is generally small and will pass only a
limited range of spatial and temporal frequencies.
In the case of a spike in the data,
inversion for the noise with a small filter does not allow the complete
restoration of the spike.
Because the noise is expected to be almost white
and in some cases dominated by spikes,
initializing ![]() to
to ![]() improves the calculation of
improves the calculation of
![]() and reduces the number of iterations needed.
and reduces the number of iterations needed.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) expressed as a minimization of
the residual
) expressed as a minimization of
the residual ![]() is
is
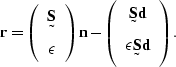
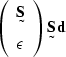
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to produce, with some simplification,
) to produce, with some simplification,
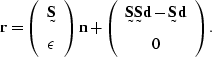
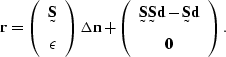
![]() .At the moment, the optimum value of
.At the moment, the optimum value of ![]() is uncertain.
It would seem that
is uncertain.
It would seem that ![]() should decrease as the signal-to-noise
ratio decreases, since the difference between the actual noise
should decrease as the signal-to-noise
ratio decreases, since the difference between the actual noise ![]() and the estimated noise
and the estimated noise ![]() is larger.
However, in the presence of strong noise,
the larger
is larger.
However, in the presence of strong noise,
the larger ![]() is, the more stable the inversion should be.
If
is, the more stable the inversion should be.
If ![]() is relatively large, around 1.0,
the amplitudes of the reflections are preserved and spurious events
are somewhat suppressed.
As
is relatively large, around 1.0,
the amplitudes of the reflections are preserved and spurious events
are somewhat suppressed.
As ![]() gets very large, the result approaches the prediction
filter result.
When
gets very large, the result approaches the prediction
filter result.
When ![]() gets small, the amplitudes of the reflectors are
attenuated, since the signal filter
gets small, the amplitudes of the reflectors are
attenuated, since the signal filter ![]() does not perfectly annihilate
the signal before the inversion.
For small
does not perfectly annihilate
the signal before the inversion.
For small ![]() , the spurious events tend to return also.
The best value of
, the spurious events tend to return also.
The best value of ![]() appears to be different for samples with Gaussian noise than
for samples with uniformly distributed noise.
For most work, it appears that good values of
appears to be different for samples with Gaussian noise than
for samples with uniformly distributed noise.
For most work, it appears that good values of ![]() vary
from 0.1 to 3.0.
Small values of
vary
from 0.1 to 3.0.
Small values of ![]() remove background noise, but seem
to introduce organized noise into the calculated signal.
For the real data examined,
the background noise increases as
remove background noise, but seem
to introduce organized noise into the calculated signal.
For the real data examined,
the background noise increases as ![]() increases,
and the continuity of the data increases as
increases,
and the continuity of the data increases as ![]() decreases.
Further work is needed to determine how the strength and type
of noise affects the value of
decreases.
Further work is needed to determine how the strength and type
of noise affects the value of ![]() .
.![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The filter
.
The filter ![]() is calculated from the data to predict the flat event.
When
is calculated from the data to predict the flat event.
When ![]() is applied to the spike, the filter response can be seen
in the prediction-filter result.
The inversion prediction result has effectively eliminated the filter response.
is applied to the spike, the filter response can be seen
in the prediction-filter result.
The inversion prediction result has effectively eliminated the filter response.