Shortcomings of prediction filtering

High-amplitude noise produces flaws in prediction-filtering techniques such as t-x and f-x prediction filtering. One flaw is the reduction of reflection amplitudes. Another is the generation of spurious events, as seen in the previous chapter and in Abma 1994. Both these errors are due to the corruption of the signal-prediction filter by the noise in the data from which the filter is calculated.

Another, less obvious, flaw in prediction filtering is that, even with a filter that perfectly predicts the signal, the output of this filtering does not perfectly separate the signal and noise. To demonstrate this, I define $\sv d$ as the available data, $\sv s$ as the signal, and $\sv n$ as the noise. The relationship between the data, the signal, and the noise is defined to be $\sv d=\sv s+\sv n$.Although the prediction of the signal could be stated otherwise, the prediction is done here with a signal annihilation filter $\st S$.The filter $\st S$ is a purely lateral 2- or 3-dimensional filter as discussed in chapter . If the signal $\sv s$ is prefectly predictable, the filter $\st S$ completely removes the signal so that $\st S \sv s =\sv 0$.In fact, only an approximate signal annihilation filter is generally available so that $\st S \sv s \approx \sv 0$,but to simplify the following discussion, $\st S \sv s =\sv 0$ will be assumed for now. When the data $\sv d$ is filtered by the exact signal annihilation filter, the result is $\st S \sv d = \st S \sv s + \st S \sv n$, which becomes $\st S\sv d = \st S\sv n$, since $\st S \sv s =\sv 0$.Since prediction filtering defines the noise as $\st S\sv d$,a filtered version of the noise $\st S \sv n$ is obtained from the prediction filtering instead of the actual noise $\sv n$.

Prediction filtering makes the assumption that the noise $\sv n$ is unaffected by the signal annihilation filter $\st S$.The difference between $\st S \sv n$ and $\sv n$ may also be seen as an inconsistency between definitions of the noise in the expressions $\sv n =\sv d -\sv s$ and $\sv n = \st S \sv d$ Soubaras (1994). For weak noise and large filters, the assumption that the noise $\sv n$ is unaffected by the signal annihilation filter $\st S$ is reasonable. For strong noise and short filters, the response of the noise to the filter is important. Although prediction filters may be made as large as desired, Chapters  and  show that large filters allow more noise to pass into the signal and that filters that are large along the time axis tend to create spurious events. For very large noises, the filter response is alway significant.

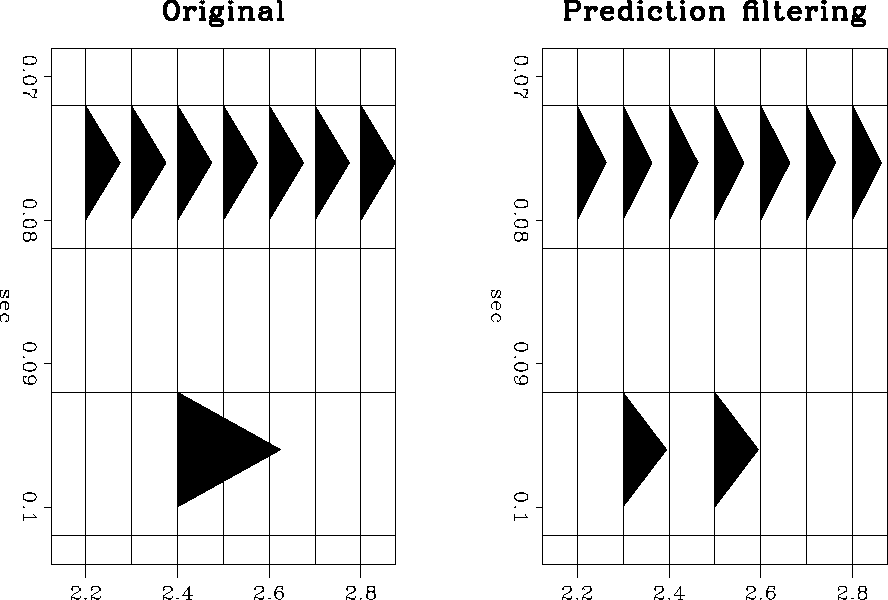
An example of the filter response to noise is shown in Figure . In the original data seen in this figure, the signal is a flat event and the noise is an isolated spike. Since the prediction filter is applied in two directions, the response of the signal annihilation filter $\st S$ can be seen on both sides of the spike's position in the prediction-filter result. The prediction-filtering result also shows a small amplitude loss in the flat event. The corruption of the signal annihilation filter $\st S$ by the spike causes this amplitude loss.

 

respn
Figure 1 The action of a prediction filter on a flat layer and a spike.

Getting a more accurate calculation of the noise requires solving the expression $\st S\sv d = \st S\sv n$ when $\st S \sv s =\sv 0$.If the exact signal annihilation filter is not available and $\st S \sv s \approx \sv 0$, the noise must be solved for from the regression $\st S\sv n \approx \st S\sv d$.Similar expressions have been used for noise removal by Claerbout and Abma 1994 and Abma and Claerbout 1994. In the next section I will present a solution to $\st S\sv n \approx \st S\sv d$.