




Next: Integration limits
Up: Introduction
Previous: First definition: MZO by
Hale (1984) starts with the prestack migration equation in
common-midpoint and offset coordinates and tries to
isolate four major processing steps.
The four steps are
- 1.
- DMO,
- 2.
- NMO,
- 3.
- Stacking,
- 4.
- Zero-offset migration.
By considering steps 1, 2, and 3 as a single process (MZO), I isolate
only two steps:
- Migration to zero-offset.
- Zero-offset migration.
After extracting the zero-offset migration from the prestack migration
equation, we are left with the migration to zero-offset operator.
For a constant velocity,
downward continue the field p(t,h,y,z=0)
recorded at the surface, to a depth 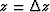
| 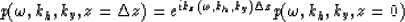 |
(7) |
for all values of 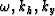 .
The prestack migration imaging step consists of
summing for all
the values of
.
The prestack migration imaging step consists of
summing for all
the values of 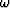 and kh after downward
continuation. To image for
t=0 and h=0:
and kh after downward
continuation. To image for
t=0 and h=0:
| 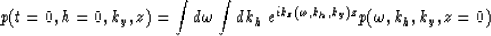 |
(8) |
where kz is given by
| ![\begin{displaymath}
{k_z(\omega,k_h,k_y)} \equiv
{ -{\omega \over v} \left\{ \le...
...2 \over {4\omega^2}}
(k_y-k_h)^2\right]^{1 \over 2} \right\} }.\end{displaymath}](img16.gif) |
(9) |
Following Hale's (1984) derivation, introduce
a new variable 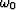 in order to
isolate the zero-offset migration operator.
The substitution is based on the equation
in order to
isolate the zero-offset migration operator.
The substitution is based on the equation
| ![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4 \omega_0^2-v^2 k_y^2}} \right]}^{1 \over 2}}.\end{displaymath}](img18.gif) |
(10) |
Substituting 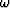 in equation (9)
the downward continuation operator
in equation (9)
the downward continuation operator 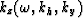 is transformed into
is transformed into
| ![\begin{displaymath}
k_z \equiv
-{ {2 \omega_0} \over v} {\left[ 1 -
{{v^2 k_y^2} \over {4 \omega_0^2}} \right]}^{1 \over 2}\end{displaymath}](img20.gif) |
(11) |
The downward continuation operator now has the same form as the
one for zero-offset. In order to isolate the zero-offset
migration operator, the variable
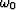 is substituted for
is substituted for 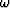 and then the order
of integration is changed between
and then the order
of integration is changed between 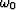 and kh.
The integration boundaries have to be observed carefully.
and kh.
The integration boundaries have to be observed carefully.





Next: Integration limits
Up: Introduction
Previous: First definition: MZO by
Stanford Exploration Project
11/17/1997
![]()
![\begin{displaymath}
{k_z(\omega,k_h,k_y)} \equiv
{ -{\omega \over v} \left\{ \le...
...2 \over {4\omega^2}}
(k_y-k_h)^2\right]^{1 \over 2} \right\} }.\end{displaymath}](img16.gif)
![]() in order to
isolate the zero-offset migration operator.
The substitution is based on the equation
in order to
isolate the zero-offset migration operator.
The substitution is based on the equation
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4 \omega_0^2-v^2 k_y^2}} \right]}^{1 \over 2}}.\end{displaymath}](img18.gif)
![\begin{displaymath}
k_z \equiv
-{ {2 \omega_0} \over v} {\left[ 1 -
{{v^2 k_y^2} \over {4 \omega_0^2}} \right]}^{1 \over 2}\end{displaymath}](img20.gif)
![]() is substituted for
is substituted for ![]() and then the order
of integration is changed between
and then the order
of integration is changed between ![]() and kh.
The integration boundaries have to be observed carefully.
and kh.
The integration boundaries have to be observed carefully.