




Next: Second definition: MZO extracted
Up: Introduction
Previous: Introduction
Both Hale and Zhang separate the NMO correction from the DMO
correction. However for variable velocity media this can not
be done, and in order to generalize the NMO DMO operation
the migration to zero-offset (MZO) concept has to be used.
Migration to zero-offset is the process that transforms a
nonzero-offset (constant offset) section into a zero-offset
section. In constant velocity media MZO = NMO+DMO.
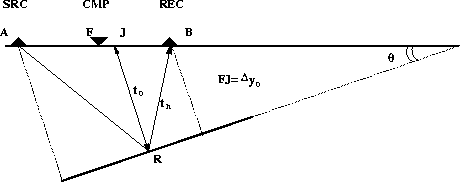
MZOdip
Figure 1 Geometry for a dipping reflector in a constant velocity medium.
The zero-offset ray JR and the nonzero-offset ray bounce
at the same reflection point R.
The dipping angle is 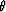 .
.

Taking into account the geometry in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the MZO correction in constant velocity media is
the MZO correction in constant velocity media is
| 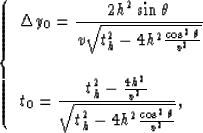 |
(1) |
where h is the half offset, t0 is twice the zero-offset travel
time from the reflection point to the surface, v is the velocity
of the medium and th is the constant-offset travel time.
The MZO correction for a given dip 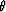 is
is
| 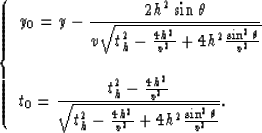 |
(2) |
To clarify the sign convention for the spatial coordinate in equation
(2), we can notice that the
y-axis is oriented to the left, and
the angles are positive if the reflector dips toward the right
and negative if the reflector
dips toward the left. In Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the angle
the angle
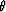 is negative. This can be also derived from the equation
is negative. This can be also derived from the equation
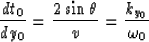
where the sign of dy0 determines the sign of the angle 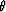 .
.
The differentials of the new variables are
| 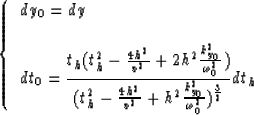 |
(3) |
The 2-D Fourier transform of the zero-offset field is
| 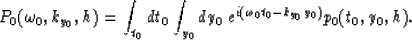 |
(4) |
Following Hale's (1984) technique,
replace the variables t0 and y0 in
equation (4)
with their expression in equation (2).
Fortunately, it is
not necessary to express explicitly th=th(t0,y0) and
y=y(t0,y0), though the respective dependencies are assumed.
After replacing the variables y0 and t0 in
equation (4), the migration to zero-offset transformation
becomes
| 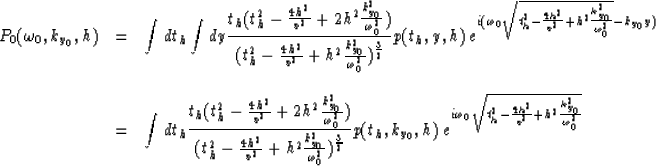 |
(5) |
Note that by replacing the quantity
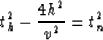
in equation (5), we get the same phase as the one obtained
by Hale and Zhang, but the Jacobian differs from Zhang's Jacobian
by a factor
| 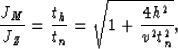 |
(6) |
which corresponds to the Jacobian of the NMO transformation.





Next: Second definition: MZO extracted
Up: Introduction
Previous: Introduction
Stanford Exploration Project
11/17/1997

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the MZO correction in constant velocity media is
the MZO correction in constant velocity media is
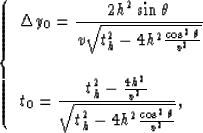
![]() is
is
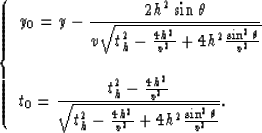
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) the angle
the angle
![]()
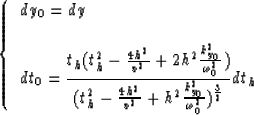
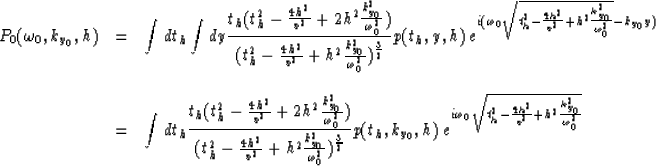
![]()