




Next: Integration order
Up: Introduction
Previous: Second definition: MZO extracted
From now on for simplicity I will use the variables
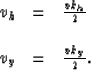
In equation (8), the values of the constant kz
have to be real. Imaginary values of kz do not
satisfy the downward continuation ordinary differential
equation:
| 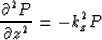 |
(12) |
and have to be excluded. Real values of kz
from equation (9) require both of the following
conditions to be satisfied:
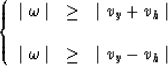
which can be reduced to the condition
| 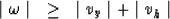 |
(13) |
Therefore, equation (8) should be written
| 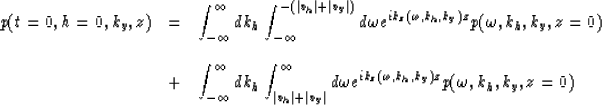 |
(14) |
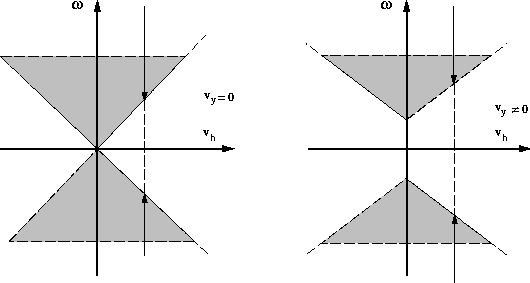
For each value of vy the integration in 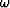 is done
in two regions: under the value
is done
in two regions: under the value
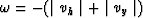 and
over the value
and
over the value 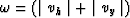 as displayed in Figure
as displayed in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
khkyomega
.
khkyomega
Figure 2 Regions of integration.

Before substituting the new variable 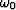 in the prestack
migration equation let us analyze the limits of integration for
the new variable
in the prestack
migration equation let us analyze the limits of integration for
the new variable 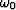 .From Appendix A, the expression of
.From Appendix A, the expression of 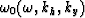 is
is
| ![\begin{displaymath}
\omega_0^2 = {1 \over 2}
\left [{ \omega^2+v_y^2-v_h^2 +
{\sqrt {(\omega^2+v_y^2-v_h^2)^2-4 \omega^2 v_y^2}}} \right ]\end{displaymath}](img29.gif) |
(15) |
and the boundary values for 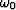 corresponding
to the limits for
corresponding
to the limits for 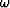 in equation (13):
in equation (13):
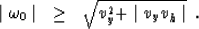





Next: Integration order
Up: Introduction
Previous: Second definition: MZO extracted
Stanford Exploration Project
11/17/1997
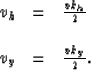
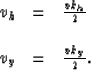
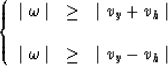
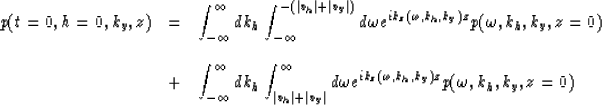
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![]() in the prestack
migration equation let us analyze the limits of integration for
the new variable
in the prestack
migration equation let us analyze the limits of integration for
the new variable ![]() .From Appendix A, the expression of
.From Appendix A, the expression of ![]() is
is
![]()