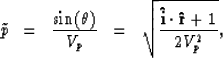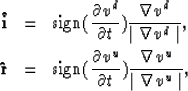Next: A SYNTHETIC EXAMPLE
Up: IMAGING CONDITION AND LOCAL
Previous: Imaging condition for the
Inversion methods which use the directional dependence of the reflection
coefficient to estimate the elastic parameters of the medium (AVO inversion)
use in general an angular functionality to express such a dependence.
This choice is not the more convenient because the angle estimation
is strongly dependent on the macro model that was used in the estimation
process. Moreover, the propagation angles depend on the elastic perturbations
that it is been used to estimate. A more appropriate choice for expressing the
directional dependence of the reflection coefficient is the local
Snell parameter, which is defined as the component of the slowness
parallel to the ``reflector plane" at each position of the underground.
Evidently, not all points of the subsurface can be considered
as a reflector, but at all points of interest; that is, where the
the upcoming wavefronts intercepts the downgoing wavefront, a ``reflector
plane can be defined". As defined, the local Snell parameter is
conserved for any perturbation in the local elastic parameters. Although
its estimated value will be still dependent on the macro model, it will
be much less sensitive to errors in the model than the angle.
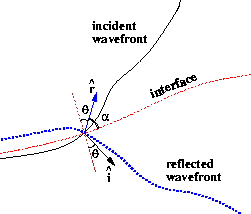
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a descending (incident) wavefield crossing
an ascending (reflected) wavefield at a given time step of the
backward propagation part of the scheme. The crossing point defines
the point of the interface that was imaged at that time, and the
angles
shows a descending (incident) wavefield crossing
an ascending (reflected) wavefield at a given time step of the
backward propagation part of the scheme. The crossing point defines
the point of the interface that was imaged at that time, and the
angles  and
and  i are measured, respectively, from the
tangent and from the normal to the interface at that point.
i are measured, respectively, from the
tangent and from the normal to the interface at that point.
reflect
Figure 1 The points where the ascending and descending wavefronts overlap
define the location of the reflector. The reflection angle can
be determined by the gradients of the two wavefields at the reflection
point, at the time when the reflection occurred.
|
|  |

From the figure we get the following relation,
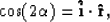
where the unit vectors 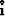 and
and 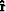 represent,
respectively, the directions of incidence and reflection.
I define the local Snell parameter
represent,
respectively, the directions of incidence and reflection.
I define the local Snell parameter 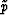 as the slowness
component parallel to the interface at the reflection point
as the slowness
component parallel to the interface at the reflection point
| 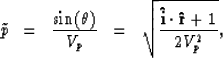 |
(3) |
where Vp is the P wave group velocity at that particular location.
This definition is restricted to an isotropic assumption, but
a more general definition can be formulated that includes the
anisotropic extension of Snell's law.
The unit vectors 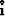 and
and 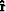 are estimated from the
particle velocity field, by using the following equations:
are estimated from the
particle velocity field, by using the following equations:
| 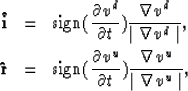 |
|
| (4) |
where vd and vu are, respectively, the downgoing and the upcoming
scalar particle velocity wavefields, defined by the equation
The sign of the time derivative in equation (4) is
calculated by
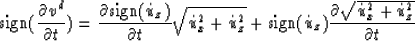
which results in
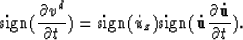





Next: A SYNTHETIC EXAMPLE
Up: IMAGING CONDITION AND LOCAL
Previous: Imaging condition for the
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a descending (incident) wavefield crossing
an ascending (reflected) wavefield at a given time step of the
backward propagation part of the scheme. The crossing point defines
the point of the interface that was imaged at that time, and the
angles
shows a descending (incident) wavefield crossing
an ascending (reflected) wavefield at a given time step of the
backward propagation part of the scheme. The crossing point defines
the point of the interface that was imaged at that time, and the
angles