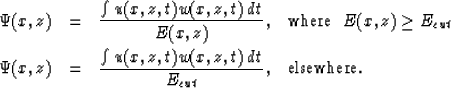Next: Computation of the local
Up: IMAGING CONDITION AND LOCAL
Previous: IMAGING CONDITION AND LOCAL
Migration includes two distinct steps: downward extrapolation in depth
or backward extrapolation in time, and imaging for the desired attribute.
When the desired attribute is the reflectivity, Claerbout's imaging principle
(Claerbout, 1971) represents the basis for many imaging condition equations.
According to this principle, a reflector exists at a point where the
upcoming and the downgoing wavefields coincide in time and space.
Jacobs (1982) compared three different ways to implement this principle in
pre-stack profile migration in the  domain:
domain:
| 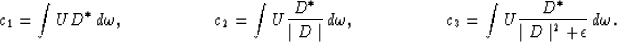 |
(1) |
His conclusion was that c3, though theoretically more correct
for estimating the reflection coefficient, was too noise sensitive to be
used in that migration scheme.
Hildebrand (1987) used a variation of this principle to image
for the acoustic impedance rather than the reflection coefficient, using
reverse-time migration to extrapolate the pressure and particle-velocity
wavefields.
Most imaging methods described in the literature involve the correlation
between scalar wavefields. An exception is the tensorial imaging
condition formulated by Karrenbach (1991):
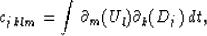
where cjklm can be interpreted as the reflectivity function
associated with the corresponding stiffness component.
Although this equation gives a more complete picture of
the subsurface, I decided to focus attention on the P-P reflectivity by
using a scalar imaging condition similar to c3 in equation (1):
| 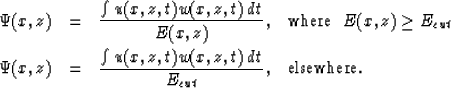 |
|
| (2) |
Equation (2) gives the correct estimation of the reflection
coefficient in the regions well illuminated by the source
(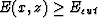 ) and a damped estimation in the dim regions.
) and a damped estimation in the dim regions.





Next: Computation of the local
Up: IMAGING CONDITION AND LOCAL
Previous: IMAGING CONDITION AND LOCAL
Stanford Exploration Project
12/18/1997
![]() domain:
domain:
![]()