




Next: GROUP-DOMAIN ALGORITHMS
Up: Karrenbach: Double elliptic scalar
Previous: MODELING AND IMAGING
Algorithms in the 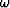 -k domain, such as Stolt's and phase-shift,
lend themselves perfectly
to anisotropic extension, since such algorithms use the dispersion relation
explicitly for downward continuation and imaging. In general the agreement
between the exact transverse isotropic (TI) dispersion relation
and the double elliptic approximation, equation 1,
is very good. The approximate algorithm is even able to model
triplications. Figures
-k domain, such as Stolt's and phase-shift,
lend themselves perfectly
to anisotropic extension, since such algorithms use the dispersion relation
explicitly for downward continuation and imaging. In general the agreement
between the exact transverse isotropic (TI) dispersion relation
and the double elliptic approximation, equation 1,
is very good. The approximate algorithm is even able to model
triplications. Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compare modeling and
migration impulse responses.
The right column plots the difference between the results in the left and
middle columns using the same scale.
Only the P and SV wave types show some small differences, while the SH wave is
exact.
The approximation fits the dispersion relation exactly on the vertical
and horizontal axes.
The largest discrepancy is in the area of triplication.
The crucial test, however,
is to model a TI media
using the exact dispersion relation and then migrate it with the
double elliptic approximation. Figure
compare modeling and
migration impulse responses.
The right column plots the difference between the results in the left and
middle columns using the same scale.
Only the P and SV wave types show some small differences, while the SH wave is
exact.
The approximation fits the dispersion relation exactly on the vertical
and horizontal axes.
The largest discrepancy is in the area of triplication.
The crucial test, however,
is to model a TI media
using the exact dispersion relation and then migrate it with the
double elliptic approximation. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that,
more or less, the correct spikes are obtained.
The middle column shows migration results, where both, modeling and
migration, used the exact dispersion relation.
The right column shows migration results where the exact form was used
for modeling and the approximation was used for imaging. The
algorithm, which uses the exact dispersion relation, reproduces the
spike, which is convolved with a ricker wavelet, very well. The double
elliptic approximation shows the spikes slightly blurred.
The results suggest that
phase domain algorithms can be expected to perform reasonably well, when
used to image an anisotropic scalar eigenfield.
shows that,
more or less, the correct spikes are obtained.
The middle column shows migration results, where both, modeling and
migration, used the exact dispersion relation.
The right column shows migration results where the exact form was used
for modeling and the approximation was used for imaging. The
algorithm, which uses the exact dispersion relation, reproduces the
spike, which is convolved with a ricker wavelet, very well. The double
elliptic approximation shows the spikes slightly blurred.
The results suggest that
phase domain algorithms can be expected to perform reasonably well, when
used to image an anisotropic scalar eigenfield.





Next: GROUP-DOMAIN ALGORITHMS
Up: Karrenbach: Double elliptic scalar
Previous: MODELING AND IMAGING
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compare modeling and
migration impulse responses.
The right column plots the difference between the results in the left and
middle columns using the same scale.
Only the P and SV wave types show some small differences, while the SH wave is
exact.
The approximation fits the dispersion relation exactly on the vertical
and horizontal axes.
The largest discrepancy is in the area of triplication.
The crucial test, however,
is to model a TI media
using the exact dispersion relation and then migrate it with the
double elliptic approximation. Figure
compare modeling and
migration impulse responses.
The right column plots the difference between the results in the left and
middle columns using the same scale.
Only the P and SV wave types show some small differences, while the SH wave is
exact.
The approximation fits the dispersion relation exactly on the vertical
and horizontal axes.
The largest discrepancy is in the area of triplication.
The crucial test, however,
is to model a TI media
using the exact dispersion relation and then migrate it with the
double elliptic approximation. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that,
more or less, the correct spikes are obtained.
The middle column shows migration results, where both, modeling and
migration, used the exact dispersion relation.
The right column shows migration results where the exact form was used
for modeling and the approximation was used for imaging. The
algorithm, which uses the exact dispersion relation, reproduces the
spike, which is convolved with a ricker wavelet, very well. The double
elliptic approximation shows the spikes slightly blurred.
The results suggest that
phase domain algorithms can be expected to perform reasonably well, when
used to image an anisotropic scalar eigenfield.
shows that,
more or less, the correct spikes are obtained.
The middle column shows migration results, where both, modeling and
migration, used the exact dispersion relation.
The right column shows migration results where the exact form was used
for modeling and the approximation was used for imaging. The
algorithm, which uses the exact dispersion relation, reproduces the
spike, which is convolved with a ricker wavelet, very well. The double
elliptic approximation shows the spikes slightly blurred.
The results suggest that
phase domain algorithms can be expected to perform reasonably well, when
used to image an anisotropic scalar eigenfield.