MODELING AND IMAGING

The double elliptic approximation allows direct conversion from the group to the phase, and vice versa; thus making it possible to consider ``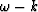$\omega-k$''or phase shift together with Kirchhoff methods. In other words movement back and forth between the wave domain and the ray domain.

Imaging procedures like Stolt's, or phase-shift incorporate anisotropic dispersion relations with ease. These algorithms explicitly require the dispersion relation in the form 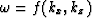$\omega= f(k_x,k_z)$, where f can be any arbitrary single-valued function. In our approximation f is a rational polynomial. Some algorithms require that the dispersion relation, Equation 1, be solved explicitly for k_z. For arbitrary f this means roots must be chosen properly and in general a numerical evaluation must be performed. In the case of the double elliptic approximation at most a third degree polynomial in k_z is obtained, for which a unique solution can be found analytically.

 

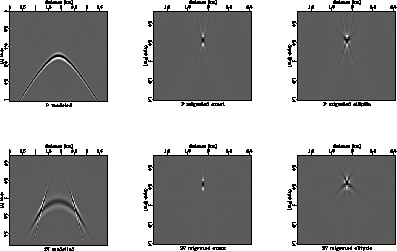
compimp
Figure 2 Scalar migration impulse response (using the Stolt method) of a TI medium is compared to the impulse response of the equivalent double elliptic approximation. The left column shows results using the exact dispersion relation, the middle column results using the double elliptic approximation, and the right column shows the difference between the two results. We are able to model even cusps to a limited extent: the approximation works very well paraxially.

 

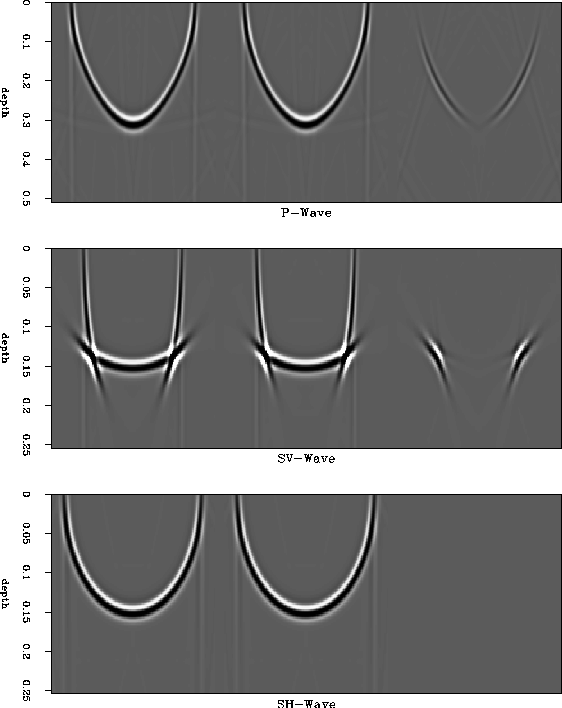
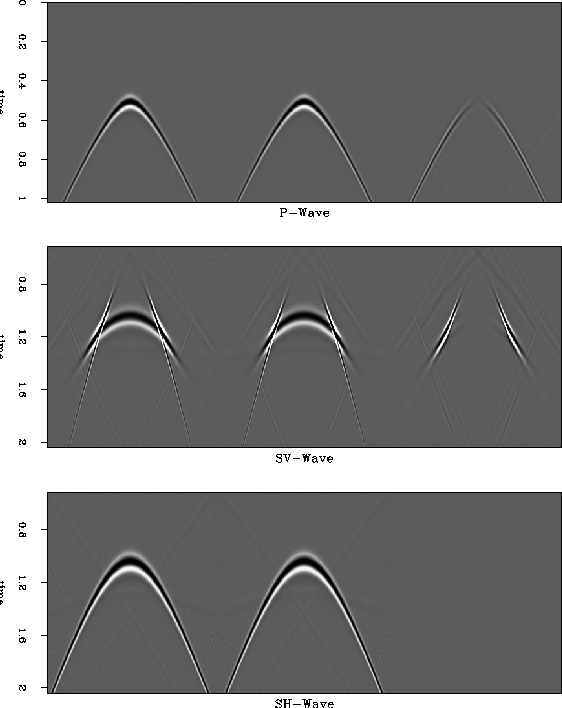
compmod
Figure 3 Scalar modeling impulse response (using the Stolt method) of a TI medium is compared to the impulse response of the equivalent double elliptic approximation. The left column shows results using the exact dispersion relation, the middle column results using the double elliptic approximation, and the right column the difference between the two. As in Figure 19,, the approximation works very well paraxially.

 

cmodmig
Figure 4 The exact scalar modeling (using the Stolt method)) of an point scatterer (left) in a TI medium is migrated once using the exact (middle) and the approximated (right) dispersion relation. The approximation works better for the P wave than for the SV wave, where it fails to collapse some energy from the cusps.