The derivation of the double elliptic paraxial approximation is described by Dellinger et al. (1991). The resulting dispersion relation in two dimensions is
| |
(1) |
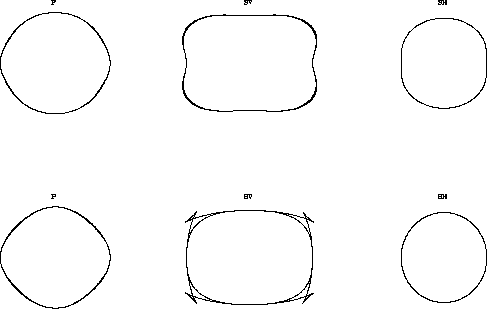
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) represents the ``phase domain''; the bottom row shows the corresponding ``group domain''. The curves are calculated from
actual stiffness constants, which are used below for modeling and migration.
I approximated in phase domain,
since I show only implementations of
phase domain algorithms in this paper.
represents the ``phase domain''; the bottom row shows the corresponding ``group domain''. The curves are calculated from
actual stiffness constants, which are used below for modeling and migration.
I approximated in phase domain,
since I show only implementations of
phase domain algorithms in this paper.
 |
Equation (1) is a very good approximation to the exact dispersion relation, when Fourier-domain algorithms, such as the Stolt or phase-shift method are used. For modeling and its transpose operation, migration, the dispersion relation must be evaluated and solved for an unknown kz. Both operations can be done quite efficiently using equation (1). The evaluation of the dispersion relation is straightforward. And when finding the kz root, we must explicitly solve a third-order polynomial in kz2.
The foregoing procedure must be seen in contrast to solving eigenvalue problems numerically or finding roots for higher order polynomials. This is the procedure that has to be followed if the dispersion relation is evaluated exactly for anisotropic media. In this context the double elliptic approximation is an efficient way to solve the problem approximately.