




Next: Prestack or poststack?
Up: Karrenbach: Double elliptic scalar
Previous: PHASE-DOMAIN ALGORITHMS
With the help of
the associated ray equation, a Kirchhoff
migration in x-t domain can be implemented directly
or traveltimes can be calculated from the dispersion relation
using anisotropic finite difference traveltimes.
Triplications are caused by concavities in the phase slowness surface.
The double elliptic approximation can model concavities well; thus
triplications are produced.
When the ray equation instead of the dispersion relation is used,
the group velocity surface is approximated instead of the phase velocity
surface. The approximation of the group velocity surface fails to follow
the triplication.
This is the fundamental difference between the 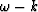 and x-t
methods. Typical x-t methods is Kirchhoff modeling and migration.
In order to be accurate, such an algorithm has to handle triplications
properly, which in general
is not as easy in x-t as in
and x-t
methods. Typical x-t methods is Kirchhoff modeling and migration.
In order to be accurate, such an algorithm has to handle triplications
properly, which in general
is not as easy in x-t as in 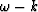 .
When the double elliptic form is used,
the exact curve cannot be approximated well in the area of
triplications.
An algorithm which uses the group domain approximation
(see Figure
.
When the double elliptic form is used,
the exact curve cannot be approximated well in the area of
triplications.
An algorithm which uses the group domain approximation
(see Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , middle bottom)
is not able to produce triplications.
, middle bottom)
is not able to produce triplications.





Next: Prestack or poststack?
Up: Karrenbach: Double elliptic scalar
Previous: PHASE-DOMAIN ALGORITHMS
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , middle bottom)
is not able to produce triplications.
, middle bottom)
is not able to produce triplications.