




Next: Other options
Up: DOWNWARD CONTINUATION IN THREE
Previous: Conjugate gradient implicit schemes
There are two methods that can be used to speed up a CG algorithm, the
use of a preconditioning matrix and estimation of a better starting
solution. The second method is the simplest to use. If some other
method is used to estimate the solution of the linear equations, the
CG algorithm can be used to refine the solution. The explicit method
is an obvious candidate to produce an initial estimate of the
solution. It is cheap and simple to implement. It does not matter that
the explicit method can become unstable because it is only used to
generate the initial solution. The final equations solved are
those of the implicit method and these equations are known to be
stable. Using an explicit solution as the input to an
iterative solution of the implicit equations, is known as the
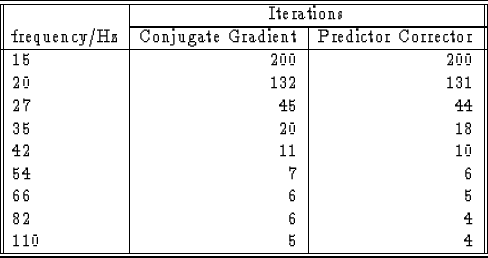
``predictor-corrector'' method. The table in Figure 5 shows
the number of iteration required for the predictor-corrector method to
converge. The explicit method used in this implementation is the one
given by equation 2. The method converges in fewer
iterations for most frequencies, but for the low frequencies it
actually takes more iterations than the simple CG method. This implies
that the explicit solution gave a worse estimate of the correct
solution than a zero vector. This is a disappointing result as I had
hoped that the predictor-corrector method would improve the
convergence of the CG algorithm at low frequencies whereas the reverse seems
to be true.
One possible reason for this can be seen by considering
the impulse response of the migration in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
data.cut
Figure 2 Impulse response of 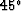 implicit migration implicit migration
|
|  |

Many of the lowest frequencies in this figure are in the top of
the heart, the highest dips having the lowest frequency content.
Since we know that this algorithm is inaccurate for dips above about
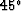 , we should not put a lot of effort into solving the
implicit equation for dips where the result is known to be wrong. One
simple way of avoiding this effect is to dip filter the input so that
high dips are not present in the data. The data should at least be
filtered so that no evanescent energy is present in the input section.
I chose to filter the input spike to attenuate dips above
, we should not put a lot of effort into solving the
implicit equation for dips where the result is known to be wrong. One
simple way of avoiding this effect is to dip filter the input so that
high dips are not present in the data. The data should at least be
filtered so that no evanescent energy is present in the input section.
I chose to filter the input spike to attenuate dips above  .The impulse response produced by migrating the filtered spike is shown
in Figure
.The impulse response produced by migrating the filtered spike is shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The table in Figure 6 shows the
number of iterations required for convergence when migrating the
filtered spike. The predictor-corrector method is now uniformly
better than the simple CG method. However, the decrease in the number
of iterations is small. The main reason is that the explicit scheme is
inaccurate at low frequencies. I would prefer a predictor step that is
accurate at low frequencies at the expense of high frequency accuracy.
The high frequencies converge rapidly without a predictor step, it is
the low frequencies that require acceleration.
. The table in Figure 6 shows the
number of iterations required for convergence when migrating the
filtered spike. The predictor-corrector method is now uniformly
better than the simple CG method. However, the decrease in the number
of iterations is small. The main reason is that the explicit scheme is
inaccurate at low frequencies. I would prefer a predictor step that is
accurate at low frequencies at the expense of high frequency accuracy.
The high frequencies converge rapidly without a predictor step, it is
the low frequencies that require acceleration.
filtdata.cut
Figure 3  implicit migration of a filtered spike implicit migration of a filtered spike
|
| 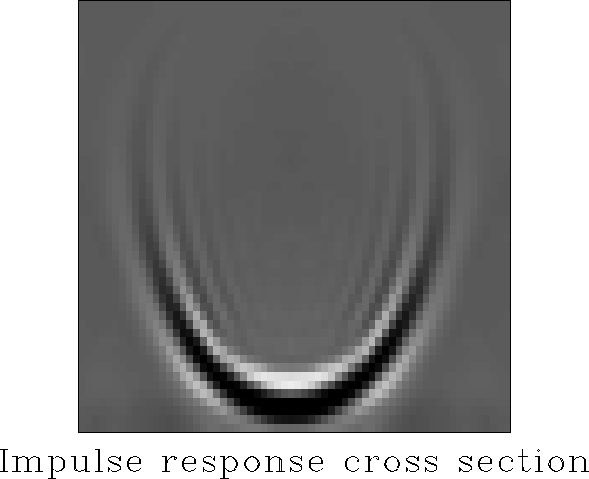 |

Figure 5:
Number of iterations required for Predictor-Corrector method to converge.
 |
Figure 6:
Number of iterations required for simple CG and predictor-corrector methods to converge when input is a dip-filtered spike. A first order Laplacian was used.
 |





Next: Other options
Up: DOWNWARD CONTINUATION IN THREE
Previous: Conjugate gradient implicit schemes
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.

![]() , we should not put a lot of effort into solving the
implicit equation for dips where the result is known to be wrong. One
simple way of avoiding this effect is to dip filter the input so that
high dips are not present in the data. The data should at least be
filtered so that no evanescent energy is present in the input section.
I chose to filter the input spike to attenuate dips above
, we should not put a lot of effort into solving the
implicit equation for dips where the result is known to be wrong. One
simple way of avoiding this effect is to dip filter the input so that
high dips are not present in the data. The data should at least be
filtered so that no evanescent energy is present in the input section.
I chose to filter the input spike to attenuate dips above ![]() .The impulse response produced by migrating the filtered spike is shown
in Figure
.The impulse response produced by migrating the filtered spike is shown
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The table in Figure 6 shows the
number of iterations required for convergence when migrating the
filtered spike. The predictor-corrector method is now uniformly
better than the simple CG method. However, the decrease in the number
of iterations is small. The main reason is that the explicit scheme is
inaccurate at low frequencies. I would prefer a predictor step that is
accurate at low frequencies at the expense of high frequency accuracy.
The high frequencies converge rapidly without a predictor step, it is
the low frequencies that require acceleration.
. The table in Figure 6 shows the
number of iterations required for convergence when migrating the
filtered spike. The predictor-corrector method is now uniformly
better than the simple CG method. However, the decrease in the number
of iterations is small. The main reason is that the explicit scheme is
inaccurate at low frequencies. I would prefer a predictor step that is
accurate at low frequencies at the expense of high frequency accuracy.
The high frequencies converge rapidly without a predictor step, it is
the low frequencies that require acceleration.

