




Next: Conclusions
Up: DOWNWARD CONTINUATION IN THREE
Previous: Predictor-corrector method
In the future I intend to try
other methods of accelerating the convergence of the CG method. The most
common way of speeding up the CG algorithm is to use a preconditioning
matrix. This is an operator, M, that is in some way approximately equivalent
to the operator A but has an inverse that is easy to compute,
( find M such that 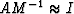 ). All that is
required of AM-1 is that it has a better condition number than A.
There are two forms for the operator that I intend to experiment with,
the split form of the 3-D operator and an incomplete Cholesky decomposition
of A.
). All that is
required of AM-1 is that it has a better condition number than A.
There are two forms for the operator that I intend to experiment with,
the split form of the 3-D operator and an incomplete Cholesky decomposition
of A.
The Cholesky decomposition of A is closely related to the work
done by Cole (1991) on Given's rotation of the 3-D operator. The
incomplete Cholesky decomposition is an approximate decomposition that has
the same sparsity structure as the original operator and is thus cheap to
compute and apply.
The preconditioned conjugate gradient method involves solving the equation
Mz = r at every iteration of the algorithm. However, the operator M does
not change between iterations so that though solving Mz=r may be
expensive (e.g., by using the split form of the operator), the
decomposed operator can be reused for every iteration.





Next: Conclusions
Up: DOWNWARD CONTINUATION IN THREE
Previous: Predictor-corrector method
Stanford Exploration Project
12/18/1997