Conjugate gradient implicit schemes

An alternative to using a direct method of solution of the pentadiagonal system is to use an iterative scheme. Cole (1989) investigated the use of Jacobi and Gauss-Seidel methods to solve the system. He found stability problems with these methods and that rates of convergence were very low for the low frequencies. The pentadiagonal system is less diagonally dominant at low frequencies. I decided to use the Conjugate Gradient method as it is guaranteed to converge for positive-definite operators. In order to use the CG method I must be able to apply the operator A and its conjugate. The operator and its conjugate are given by

$$A = \left[1+\left( {v\over{2\omega}}^2 + i{v\over{2\omega}}\delta z \right) \nabla_{xy}^2 \right] \,,$$

and

$$A^* = \left[1+\left( {v\over{2\omega}}^2 - i{v\over{2\omega}}\delta z \right) \nabla_{xy}^2 \right] \,.$$

Application of these operators involves multiplication, addition, and use of the Laplacian operator. On a mesh-connected parallel computer all these operations can be implemented efficiently, making full use of all the processors. The algorithm is unchanged if I choose to use a more accurate Laplacian operator. The only difference is that a higher order Laplacian will produce a less diagonally dominant operator so the method will converge more slowly. The cost of applying the Laplacian operator is O(n²). If the CG method is run to completion it will take n² iterations so the total cost will be O(n⁴). However, the aim is to find a set of equations that will converge to sufficient accuracy in less than the full number of iterations.

I implemented a simple CG method on the Connection Machine. I use the L₂ norm of the residuals as the indicator of convergence of the algorithm. If the ratio of the norm of the residual to the norm of the RHS of the equation was less than 10^-5, I stopped the algorithm. The test problem was a small 3-D grid. The input was 64 points in x and y with 64 time samples. The output had 50 depth samples. The second column in Figure 1 shows the number of iterations required to meet this criterion for a range of frequencies when using a Laplacian operator with three points in X and Y. The third column shows the results when using a Laplacian operator with five points in X and Y. An arbitrary limit of 200 iterations was imposed. The method converged poorly at low frequencies in both cases, with the higher order Laplacian producing a more thickly banded, less diagonally dominant, operator the convergence is even slower.

  

Figure 1: Number of iterations required for simple CG method to converge.

Figure  shows a time slice of the migration impulse response from the CG method. The impulse response is circular and does not suffer from the numerical anisotropy introduced by the splitting method.

 

filtdata.slice Figure 1 Impulse response of 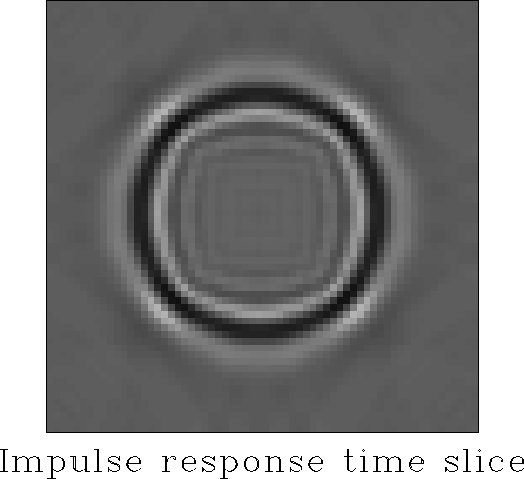$45^\circ$ implicit migration.