Running rings around Schoenberg-Muir

S&M layer averaging works for waves propagating in a stack of flat layers at any angle (although as we can see in Figure 2, the zero-frequency approximation can't be pushed as far for waves propagating along the layers as it can for waves propagating across them).

 

model
Figure 3 A typical model. The intensity on this plot shows the value of 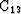${\hbox{\rm C}}_{13}$ at each gridpoint. The model is 512² gridpoints. The ring is 110 gridpoints across from inner to outer edge. The source is a vertical point force at the ``*''.

What about a stack of dipping layers? Schoenberg-Muir theory says nothing about the boundary conditions on the ends of the layers; the math assumes infinite flat layers so that the troublesome ends are infinitely far away and can be ignored. Oblique stacks of layers, like a canted row of dominos, violate this assumption because the waves must encounter the edges of the layers to enter the stack. (See Figure 1.) Does this violation of the underlying assumptions cause noticeable effects? Figure 3 shows a 512² gridpoint model consisting of a annulus-shaped set of layers embedded in its homogeneous S&M equivalent medium. (The layers are chosen the same way as in Figure 2.) S&M theory tells us that if the wavelength of the source is sufficiently long, and the edge effects of the layers are ignored, the waves should emerge from the stack looking the same as they would if the medium were homogeneous everywhere. Figure 4 shows the actual results; the qP wave is low enough in spatial frequency to work nearly perfectly for all angles of propagation. The main difference is that the amplitude of the qP wave in the layered model is about 10% lower. The edge effects do not seem to be significant in this model.

 

blob
Figure 4 Left: Snapshots of waves propagating in the annulus model shown in Figure 3. The model is 512² gridpoints, the annulus is 110 gridpoints wide, the qP waves have a wavelength of about 135 gridpoints, and the qS waves have a wavelength of about 75 gridpoints. Right: The difference between waves in the S&M equivalent homogeneous model and the annulus model on the left. The two white circles mark the edges of the heterogeneous part of the model, where the differing underlying elastic constants and density between the two models makes subtracting displacements meaningless.