One dimensional filters operating on time slices in the t-x domain are implicitly estimating the spatial spectrum of the data. If there are multiple dips present in the data they cannot be separated on the basis of their spatial spectrum alone. There are two possible solutions to this problem, transform the time axis to the frequency domain and work with constant frequency slices. This is the method used in f-x filter design (see for example Canales,1984). The other approach is to design two dimensional filters. I have chosen to use two dimensional interpolation error filters.
The 2-D filters will estimate the spectrum of the data in both time and space. The 1-D filters that I have described up to now are a special case of the 2-D filter. The notation used earlier may be preserved except now the vectors k and u of known and unknown data become 2-D arrays, the filter f becomes a 2-D operator and * denotes 2-D convolution. The model parameters are now the unknown data points within some 2-D window and the coefficients of a 2-D interpolation error filter.
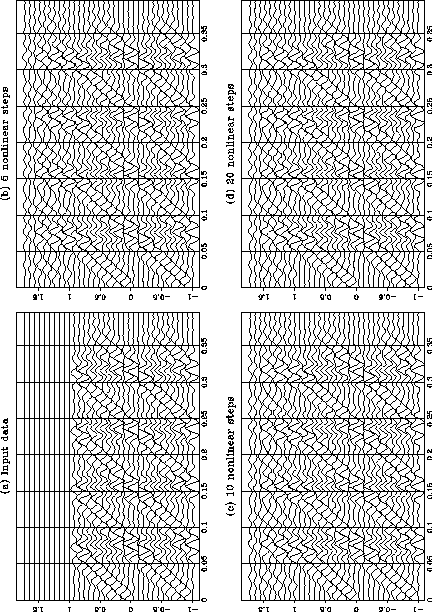
Figure 7 illustrates a case where we might expect the 1-D algorithm to fail, the input dataset has two conflicting dips, one flat and the other
dipping at 
. The linear 1-D process extends only the horizontal energy. The nonlinear 1-D process does not successfully extend both dips.
 |
If a 2-D algorithm is applied with a filter half length of 4 samples in both x and t the output, shown in figure 8, is not very different to the output of the nonlinear 1-D algorithm. One possibility is that more iterations might be needed to make the problem converge. However the cost of the 2-D algorithm is already much more than the 1-D algorithm so I decided to try another approach.
 |