To apply the estimation procedure using interpolation error filters I must minimize
![]()
![]()
![]()
![]()
At each step of the non-linear algorithm I solve the linear problem for the
model parameters ![]() and
and ![]() and then update the estimates
of the filter coefficients and missing samples by
and then update the estimates
of the filter coefficients and missing samples by
![]()
Figure 4 illustrates a case where the linear estimation does not work, there are dips present on the input data. The local smoothness assumption that I made in deriving the linear interpolation process is violated. When I interpolate using the linear operator the dips are not preserved, as seen in the second panel. The nonlinear operator shown in the third panel preserves the spatial spectrum of the input time slices and therefore preserves the dip in the interpolated region. The fourth panel shows the results for the case where the filter is designed on a 10 row window of the data. This should ensure stability in cases where there is noise present in the input.
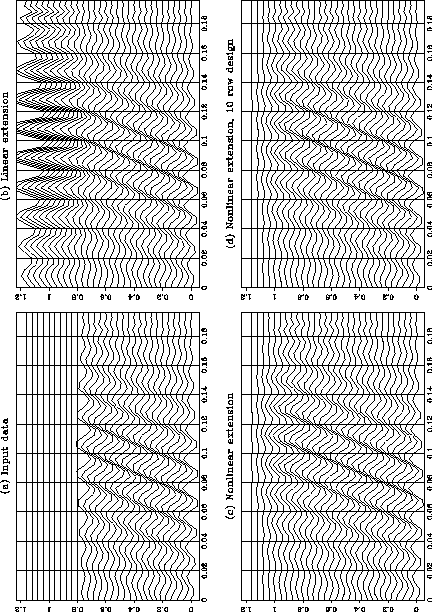 |
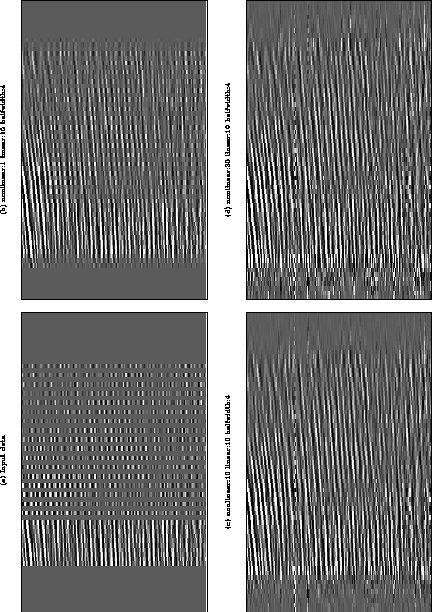
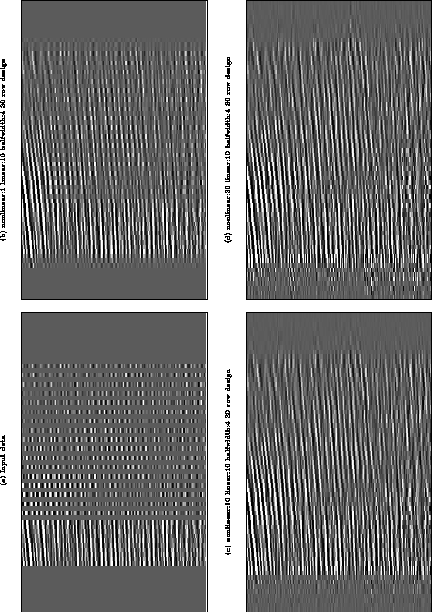
Figure 5 shows the results of applying the nonlinear process to real data. The results generally improve as more nonlinear iterations are performed. Some time slices have extensions that appear to have a different character to the neighboring time slices. This is caused by anomalous amplitudes in the input data. If I stabilize the filter design by estimating it on 20 rows at a time I obtain the more uniform results shown in figure 6
 |
 |