




Next: Multiple dips
Up: Nichols: Estimation of missing
Previous: TWO DIMENSIONAL INTERPOLATION ERROR
Jon Claerbout suggested that I should use a filter that had the property
that it would destroy plane waves of a given dip. Given such an operator I could perform a joint estimation of the local dip and the missing data values.
He suggested a form for such a filter, which he calls the ``plane wave destruction'' filter or the ``wavekill'' operator.
I can reject a dip, p, with the operator,
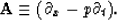
An approximation to this operator can be implemented on a  differencing star.
The best estimate of the dip of an array of data can be found by minimizing
differencing star.
The best estimate of the dip of an array of data can be found by minimizing
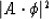
If  is the array
is the array 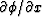 and
and 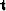 is the array
is the array
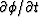 then the minimum value of
then the minimum value of 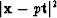 is at
is at 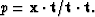
To use this operator for interpolation when the dip is known
I minimize the residual,
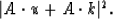
This is a linear least squares problem of the type described earlier.
If the dip is not known I have to solve a non-linear problem for both the dip and the missing data values.





Next: Multiple dips
Up: Nichols: Estimation of missing
Previous: TWO DIMENSIONAL INTERPOLATION ERROR
Stanford Exploration Project
1/13/1998
![]()
![]()
![]()