|
|
|
|
Effective medium theory for elastic composites |
A great variety of effective medium theories exist for studies of the elastic properties of composites. Of these theories, the scattering theory presented by Zeller and Dederichs (1973), Korringa (1973), and Gubernatis and Krumhansl (1975) have the most in common with the scattering-theory approach presented here. However, the present approach appears to be unique among the self-consistent scattering-theory variety, being dynamic (i.e., frequency dependent), while all the others are based on static or quasi-static derivations. This difference becomes a very useful advantage if we want to generalize the approach to finite (nonzero) frequencies, as is required for viscoelastic media. The bounding arguments presented here do not carry over directly to the frequency dependent case, but they actually can be generalized -- as shown by Gibianksy and Milton (1993), Milton and Berryman (1997), and Gibiansky et al. (1999).
Another class of effective medium theories studied by Hill (1965), Budiansky (1965), Wu (1966), Walpole (1969), and Boucher (1974) does not yield the same results as the present one, except for the case of spherical inclusions. It has been shown elsewhere [Berryman (1980b)] how the derivation of the approach of Hill, Budiansky, and others can be kinds of symmetrized to yield the symmetrical results as presented here that I prefer. Since the CPA class of effective medium theories gives results equivalent to the Hashin-Shtrikman [Hashin and Shtrikman (1963,1961,1962)] bounds when the inclusions are disk-shaped, I conclude that these results are preferred - since they do satisfy these bounding constraints, while the alternatives do not. The numerical results show general satisfaction of the bounds.
To elucidate somewhat further the relationship between the static and dynamic derivations of the effective
medium results, I will outline the static derivation next. The integral equations
for the static strain field are given by
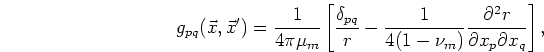 and
and
Iterating Equation (46), I obtain the well-known Born series
Equation (51) is now in a convenient form for use in determining the
effective elastic tensor ![]() of a composite defined by
of a composite defined by
In principle, Equation (56) provides an exact solution for the effective moduli.
However, the total ![]() -matrix itself is generally too difficult to calculate. It turns out to be
more reasonable and more effective [Velicky et al. (1968)] to rearrange
the terms of the total
-matrix itself is generally too difficult to calculate. It turns out to be
more reasonable and more effective [Velicky et al. (1968)] to rearrange
the terms of the total ![]() -matrix into a series of terms with repeated scattering from
individual scatterers (
-matrix into a series of terms with repeated scattering from
individual scatterers (![]() ). Then, by setting the ensemble average of the individual
). Then, by setting the ensemble average of the individual
![]() matrices to zero
matrices to zero
When the constituents and the composite as a whole are all relatively homogeneous and isotropic, the tensor
Equation (57) reduces to two coupled equations:
|
|
|
|
Effective medium theory for elastic composites |