|
|
|
|
Effective medium theory for elastic composites |
In their review article, Watt et al. (1976) discuss various rigorous bounds on the
effective moduli of composites. For example, the well-known Voigt (arthimetic) and
Reuss (harmonic) averages are, respectively, rigorous [Hill (1952)] upper and lower bounds for
both ![]() and
and ![]() . Generally tighter bounds have also been given by
Hashin and Shtrikman (1963,1961,1962).
. Generally tighter bounds have also been given by
Hashin and Shtrikman (1963,1961,1962).
Still tighter bounds have been obtained in principle by Beran and Molyneux (1966) for the bulk modulus and by McCoy (1970) for the shear modulus. However, the resulting formulas depend on three-point spatial correlation functions for the composite and are therefore considerably more difficult to evaluate than the expressions for the Hashin-Shtrikman [Hashin and Shtrikman (1963,1961,1962)] bounds, which depend only on the material constants and volume fractions. Miller (1969a,b) evaluated the bounds of Beran and Molyneux (1966) by treating an isotropic homogeneous distribution of statistically independent cells. Silnutzer (1972) used the same approach to simplify the bounds of McCoy (1970) for cell materials. Furthermore, Milton (1981) has shown that the bounds of Beran and Molyneux (1966) and McCoy (1970) can be simplified somewhat even if the composite is not a cell material. Nevertheless, the bounds which are most easily evaluated are still the Hashin-Shtrikman [Hashin and Shtrikman (1963,1961,1962)] (HS) bounds, the Beran-Molyneux-Miller (BMM) bounds, and the McCoy-Silnutzer (MS) bounds. I will compare these bounds to the estimates obtained from the coherent potential approximation (CPA), the specific effective medium theory being stressed here.
To aid in the following comparisons, it is convenient to introduce two functions:
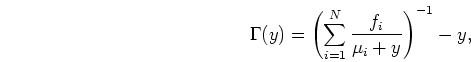 :
:
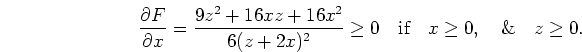 are non-negative (which will soon be shown to be
the case in these applications), it follows that
are non-negative (which will soon be shown to be
the case in these applications), it follows that
Now, if I define the minimum and maximum moduli among all the
constitutents by
The Beran-Molyneux-Miller bounds and the McCoy-Silnutzer bounds are
known for two-phase composites (i.e., ![]() ). These bounds can be written
in succinct form using the notation of Milton (1981). By defining two geometric
parameters
). These bounds can be written
in succinct form using the notation of Milton (1981). By defining two geometric
parameters
![]() and
and
![]() , and two
related averages [analogous to the volume fraction weighted average
, and two
related averages [analogous to the volume fraction weighted average
![]() ] of any modulus
] of any modulus ![]() by
by
![]() , and
, and
![]() , then the bounds can be written
very concisely as:
, then the bounds can be written
very concisely as:
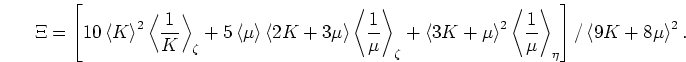 for spherical
cells,
for spherical
cells,
It is particularly simple to compare these bounds with the results of effective medium
theory when the inclusions are assumed to be spherical in shape. Then, the estimates of
the moduli are given by the self-consistent formulas (which are mutually interdependent):
The arguments just given are valid only for the case of spherical inclusions. The author knows of no general argument relating the effective medium results to the rigorous bounds for arbitrary inclusion shapes. However, as will be observed in the following Figures, numerical examples illustrate the effective medium estimates always lying between the bounds.
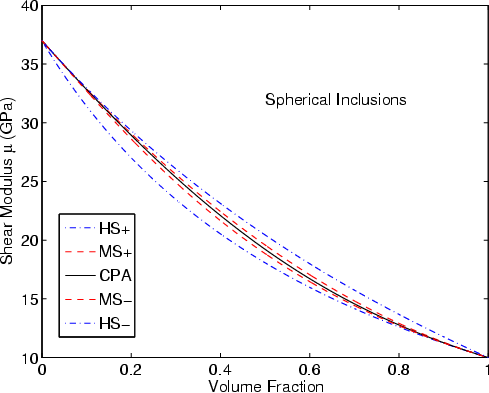
|
|---|
|
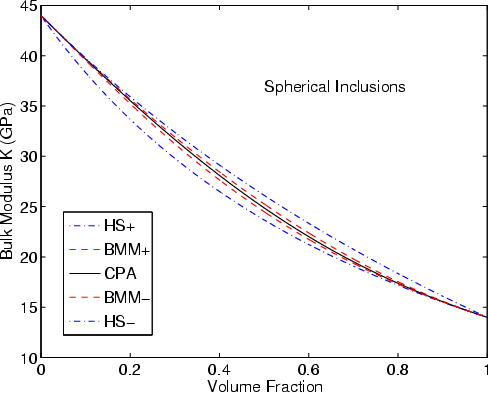
K-SPH,G-SPH
Figure 1. Estimates of the effective bulk (a) and shear (b) moduli of elastic composites with constituents |
|
|
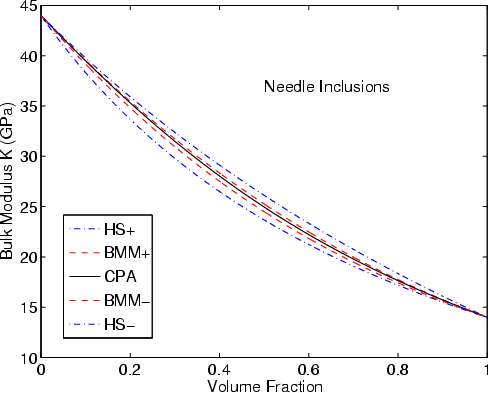
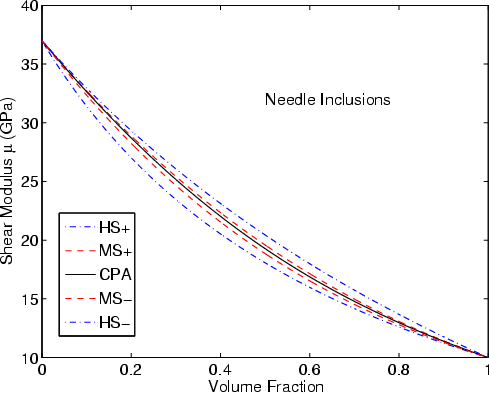
|
|---|
|
K-NDL,G-NDL
Figure 2. Estimates of the effective bulk (a) and shear (b) moduli of elastic composites with constituents |
|
|
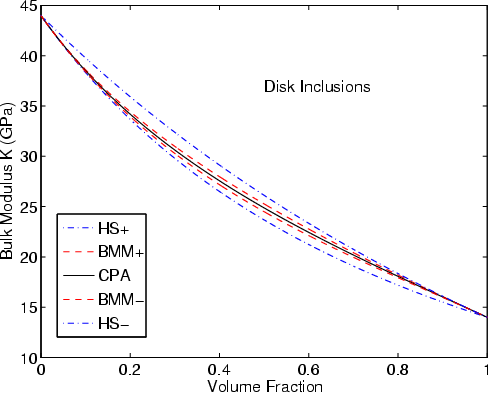
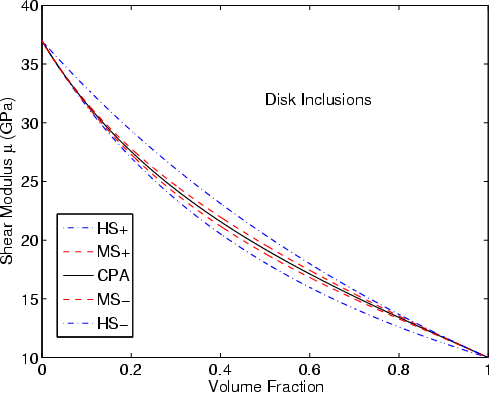
|
|---|
|
K-DSK,G-DSK
Figure 3. Estimates of the effective bulk (a) and shear (b) moduli of elastic composites with constituents |
|
|
Typical results are presented in Figures 1-3. The values of the constituents' moduli
were chosen to be: ![]() GPa,
GPa, ![]() GPa,
GPa, ![]() GPa, and
GPa, and ![]() GPa.
The values of
GPa.
The values of ![]() and
and ![]() were chosen as a compromise between two extremes:
(a) If
were chosen as a compromise between two extremes:
(a) If ![]() and
and ![]() are too close to
are too close to ![]() and
and ![]() , then the bounds are too
close together to be distinguishable on the plots. (b) If
, then the bounds are too
close together to be distinguishable on the plots. (b) If ![]() and
and ![]() are both
chosen to be zero, the iteration to the effective medium theory results does not converge
for the case of disk-like inclusions [Berryman (1980b)], although all the other cases
converge without difficulties.
I find in all cases considered that the effective medium theory results lie
between the rigorous bounds, as stated above.
are both
chosen to be zero, the iteration to the effective medium theory results does not converge
for the case of disk-like inclusions [Berryman (1980b)], although all the other cases
converge without difficulties.
I find in all cases considered that the effective medium theory results lie
between the rigorous bounds, as stated above.
|
|
|
|
Effective medium theory for elastic composites |