 |
 |
 |
 | Delayed-shot migration in TEC coordinates |  |
![[pdf]](icons/pdf.png) |
Next: Tilted elliptical-cylindrical coordinates
Up: 3D plane-wave migration
Previous: Full plane-wave phase-encoding migration
An alternate 3D migration formulation is to phase-encode individual sail lines for a given ray parameter, 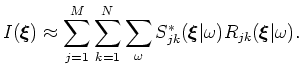 , solely according to inline source position. This phase-encoding approach is related to conical-wave migration, which requires
, solely according to inline source position. This phase-encoding approach is related to conical-wave migration, which requires  in equation 3. However, I choose to not make this restriction because it is realized only by straight sail lines and non-flip-flop sources (Liu et al., 2006). Rather, I present an alternative theory of inline delayed-shot migration that allows more general crossline source and receiver distribution.
in equation 3. However, I choose to not make this restriction because it is realized only by straight sail lines and non-flip-flop sources (Liu et al., 2006). Rather, I present an alternative theory of inline delayed-shot migration that allows more general crossline source and receiver distribution.
Inline delayed-shot wavefields, propagated through the migration domain to generate the full source and receiver wavefield volumes, are defined by
![$\displaystyle \overline{S(\boldsymbol{\xi}\vert\omega )}= \sum_{l=1}^A \sum_{j=...
...\xi}\vert\omega ) f(\omega )
{\rm e}^{ i\omega [p_{\xi_1} \Delta \xi_1 (j-p)]},$](img47.png) |
|
|
(7) |
![$\displaystyle \overline{R(\boldsymbol{\xi}\vert\omega )}= \sum_{l=1}^A \sum_{k=...
...xi}\vert\omega ) f(\omega )
{\rm e}^{ i \omega [p_{\xi_1} \Delta \xi_1 (k-p)]},$](img48.png) |
|
|
(8) |
where 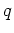 and
and 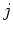 are the source and receiver inline position, respectively,
are the source and receiver inline position, respectively, 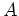 is the number of inline records,
is the number of inline records, 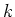 is the sail line index out of a total of
is the sail line index out of a total of 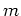 sail lines, and
sail lines, and 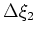 is a reference inline index.
is a reference inline index.
An image volume
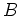 is generated from a series of inline delayed-shot migration images,
is generated from a series of inline delayed-shot migration images,
 , formed by correlating the composite inline source and receiver wavefields and stacking the results over frequency. The inline delayed-shot migration kernel mixes source and receiver wavefield energy,
, formed by correlating the composite inline source and receiver wavefields and stacking the results over frequency. The inline delayed-shot migration kernel mixes source and receiver wavefield energy,
 and
and
 , according to
, according to
Similar to plane-wave migration, mixing wavefields of differing 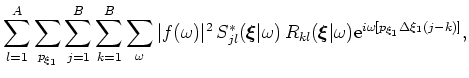 and
and  indices will introduce crosstalk into the image volume. However, inline delayed-shot migration will be crosstalk-free in the following limit:
indices will introduce crosstalk into the image volume. However, inline delayed-shot migration will be crosstalk-free in the following limit:
 |
(10) |
Defining
 and using the approximation in equation 10, I rewrite
and using the approximation in equation 10, I rewrite
 |
(11) |
Stacking over all inline delayed-shot sail-line migration results
yields the full image volume,
 |
(12) |
This proves the equivalence of inline delayed-shot and shot-profile migration.
 |
 |
 |
 | Delayed-shot migration in TEC coordinates |  |
![[pdf]](icons/pdf.png) |
Next: Tilted elliptical-cylindrical coordinates
Up: 3D plane-wave migration
Previous: Full plane-wave phase-encoding migration
2009-05-05
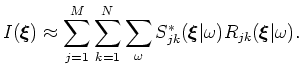 , solely according to inline source position. This phase-encoding approach is related to conical-wave migration, which requires
, solely according to inline source position. This phase-encoding approach is related to conical-wave migration, which requires ![]() is generated from a series of inline delayed-shot migration images,
is generated from a series of inline delayed-shot migration images,
 , formed by correlating the composite inline source and receiver wavefields and stacking the results over frequency. The inline delayed-shot migration kernel mixes source and receiver wavefield energy,
, formed by correlating the composite inline source and receiver wavefields and stacking the results over frequency. The inline delayed-shot migration kernel mixes source and receiver wavefield energy,
![]() and
and
![]() , according to
, according to
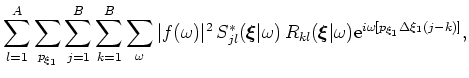 and
and  and using the approximation in equation 10, I rewrite
and using the approximation in equation 10, I rewrite