 |
 |
 |
 | Delayed-shot migration in TEC coordinates |  |
![[pdf]](icons/pdf.png) |
Next: Inline delayed-shot migration
Up: 3D plane-wave migration
Previous: 3D plane-wave migration
Performing 3D plane-wave migration is similar in many respects to 3D shot-profile migration. The main differences derive from how the composite source and receiver wavefield volumes,
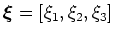 and
and
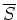 , are re-synthesized from individual source and receiver profiles,
, are re-synthesized from individual source and receiver profiles, 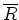 and
and 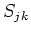 , prior to imaging. The complete wavefields are generated by filtering the source and receiver profiles by a function dependent on the inline and cross-line plane-wave ray parameters,
, prior to imaging. The complete wavefields are generated by filtering the source and receiver profiles by a function dependent on the inline and cross-line plane-wave ray parameters,
![$ \boldsymbol{p_\xi}=[p_{\xi_1}, p_{\xi_2}]$](img12.png) . These wavefields are then propagated through the migration domain to generate the full source and receiver wavefield volumes
. These wavefields are then propagated through the migration domain to generate the full source and receiver wavefield volumes
![$\displaystyle \overline{S(\boldsymbol{\xi}\vert\omega )}= \sum_{j=1}^A \sum_{k=...
...m e}^{ i\omega [p_{\xi_1} \Delta \xi_1 (j-p) + p_{\xi_2}
\Delta \xi_2 (k-q) ]},$](img13.png) |
|
|
(1) |
![$\displaystyle \overline{R(\boldsymbol{\xi}\vert\omega )}= \sum_{l=1}^A \sum_{m=...
...m e}^{ i\omega [p_{\xi_1} \Delta \xi_1 (l-p) + p_{\xi_2}
\Delta \xi_2 (m-q) ]},$](img14.png) |
|
|
(2) |
where
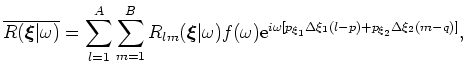 is a frequency filter to be discussed below,
is a frequency filter to be discussed below,
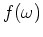 and
and
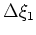 are the inline and cross-line sampling intervals,
are the inline and cross-line sampling intervals, 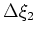 and
and 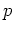 are reference spatial indices in the inline and cross-line directions,
are reference spatial indices in the inline and cross-line directions, 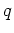 and
and 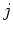 are indices fixing the inline and crossline source position,
are indices fixing the inline and crossline source position, 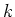 and
and 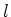 are indices fixing the inline and cross-line receiver position, and
are indices fixing the inline and cross-line receiver position, and 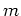 and
and 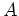 are the number of inline and cross-line source records, respectively. The phase encoding, implemented at the surface independent of wavefield extrapolation, is valid for any generalized coordinate system. Note that the wavefield propagation throughout the migration volume in equations 1 and 2 is understood, and assumed to be governed by the wavefield propagation techniques described in Shragge (2008).
are the number of inline and cross-line source records, respectively. The phase encoding, implemented at the surface independent of wavefield extrapolation, is valid for any generalized coordinate system. Note that the wavefield propagation throughout the migration volume in equations 1 and 2 is understood, and assumed to be governed by the wavefield propagation techniques described in Shragge (2008).
An image volume
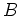 is formed from a series of individual full plane-wave migration images,
is formed from a series of individual full plane-wave migration images,
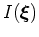 , by correlating the composite plane-wave source and receiver wavefields and stacking the results over frequency. The plane-wave migration kernel mixes source and receiver wavefield energy,
, by correlating the composite plane-wave source and receiver wavefields and stacking the results over frequency. The plane-wave migration kernel mixes source and receiver wavefield energy,
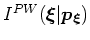 and
and
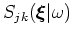 , according to
, according to
where 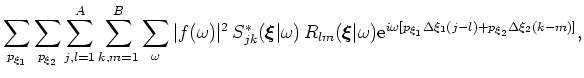 indicates complex conjugate.
indicates complex conjugate.
Generally, mixing wavefields of differing 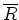 and
and 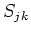 indices introduces image crosstalk. A plane-wave migration image will be crosstalk-free, though, in the following limits:
indices introduces image crosstalk. A plane-wave migration image will be crosstalk-free, though, in the following limits:
where
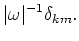 and
and
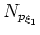 are the number of plane waves in the
are the number of plane waves in the 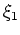 and
and 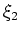 directions. Assuming that equation 4 approximately is valid (i.e., for large values of
directions. Assuming that equation 4 approximately is valid (i.e., for large values of
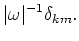 and
and
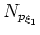 ), I rewrite equation 3 as
), I rewrite equation 3 as
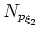 |
(5) |
which, by defining
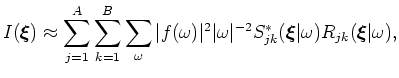 , generates the following expression:
, generates the following expression:
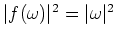 |
(6) |
This demonstrates the equivalence between plane-wave and shot-profile migration (Liu et al., 2006).
 |
 |
 |
 | Delayed-shot migration in TEC coordinates |  |
![[pdf]](icons/pdf.png) |
Next: Inline delayed-shot migration
Up: 3D plane-wave migration
Previous: 3D plane-wave migration
2009-05-05
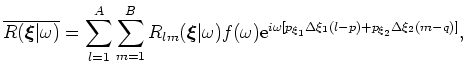 is a frequency filter to be discussed below,
is a frequency filter to be discussed below,
![]() is formed from a series of individual full plane-wave migration images,
is formed from a series of individual full plane-wave migration images,
![]() , by correlating the composite plane-wave source and receiver wavefields and stacking the results over frequency. The plane-wave migration kernel mixes source and receiver wavefield energy,
, by correlating the composite plane-wave source and receiver wavefields and stacking the results over frequency. The plane-wave migration kernel mixes source and receiver wavefield energy,
![]() and
and
![]() , according to
, according to
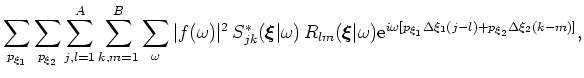 indicates complex conjugate.
indicates complex conjugate.
![]() and
and ![]() indices introduces image crosstalk. A plane-wave migration image will be crosstalk-free, though, in the following limits:
indices introduces image crosstalk. A plane-wave migration image will be crosstalk-free, though, in the following limits:
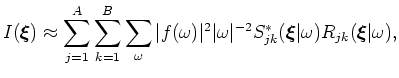 , generates the following expression:
, generates the following expression: