 |
 |
 |
 | Angle-domain common-image gathers in generalized coordinates |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Shragge: Generalized-coordinate ADCIGs
Previous: Acknowledgments
-
Lee, M. W. and S. Y. Suh, 1985, Optimization of one-way wave-equations (short
note): Geophysics, 50, 1634-1637.
-
Appendix
A
ADCIG coordinate transform
This appendix addresses how to express operators
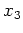 and
and
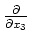 in generalized coordinate systems to derive equation 10. I first assume that generalized coordinate systems are related to the Cartesian variables through a bijection (i.e., one-to-one mapping)
in generalized coordinate systems to derive equation 10. I first assume that generalized coordinate systems are related to the Cartesian variables through a bijection (i.e., one-to-one mapping)
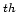 |
(26) |
with a non-vanishing Jacobian of coordinate transformation,
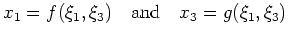 . The bijection between a generalized and Cartesian coordinate system allows us to rewrite the left-hand-sides of equations 7 as (, )
. The bijection between a generalized and Cartesian coordinate system allows us to rewrite the left-hand-sides of equations 7 as (, )
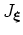 |
(27) |
Expanding the Jacobian notation leads to
![$\displaystyle \left[ \begin{array}{c}
\frac{\partial t}{\partial \xi_1}\frac{\p...
...egin{array}{c}
{\rm sin} \alpha \\
{\rm cos} \alpha
\end{array} \right].$](img100.png) |
|
|
(28) |
The right-hand-sides of equations A-3 are analogous to those derived by (). Cross-multiplying the expressions by factors
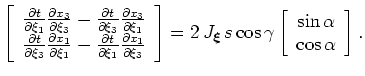 and
and
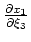
![$\displaystyle \left[ \begin{array}{c}
\frac{\partial
x_1}{\partial \xi_3}
\left...
... \\
\frac{\partial x_3}{\partial \xi_3} {\rm cos} \alpha
\end{array} \right]$](img103.png) |
|
|
(29) |
and adding the two expressions results in
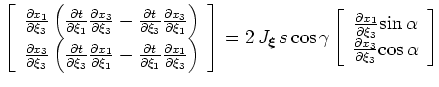 |
(30) |
A similar argument can be used to construct the equations for the subsurface-offset axis. The bijection between the generalized coordinate and Cartesian subsurface-offset axes allows for the left-hand-side of equations 7 to be rewritten as
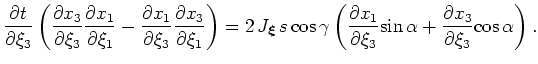 |
(31) |
where
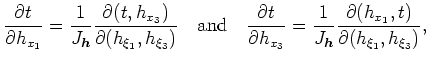 is the subsurface-offset Jacobian of transformation. Expanding the Jacobian notation leads to
is the subsurface-offset Jacobian of transformation. Expanding the Jacobian notation leads to
![$\displaystyle \left[ \begin{array}{c}
\frac{\partial t}{\partial h_{\xi_1}}\fra...
...egin{array}{c}
{\rm cos} \alpha \\
{\rm sin} \alpha
\end{array} \right].$](img107.png) |
|
|
(32) |
The right-hand-side of equations A-7 are again analogous to those given by (). Cross-multiplying the expressions by factors
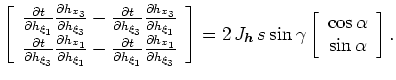 and
and
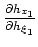
![$\displaystyle \left[ \begin{array}{c}
\frac{\partial h_{x_1}}{\partial h_{\xi_1...
...{\partial h_{x_3}}{\partial h_{\xi_1}}
{\rm sin} \alpha
\end{array} \right],$](img110.png) |
|
|
(33) |
and subtracting the two expressions above yields
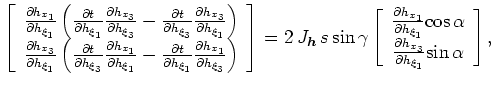 |
(34) |
An expression for ADCIGs can be obtained by dividing equation A-9 by equation A-5
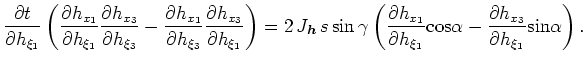 |
(35) |
One question arising from the geometric factors in equation A-10 is what do the terms
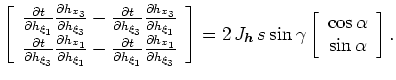 ,
,
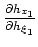 ,
,
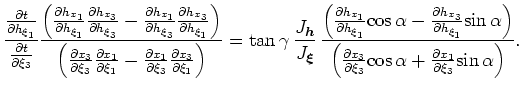 and
and
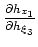 represent? I assume that the subsurface offset axes are generated by uniform wavefield shifting such that the following equations are valid:
represent? I assume that the subsurface offset axes are generated by uniform wavefield shifting such that the following equations are valid:
![$\displaystyle \left[\begin{array}{c}
h_{x_1} \\
h_{x_3} \\
h_{\xi_1}\\
h_{\x...
...x_1}{\partial \xi_3}\\
\frac{\partial x_3}{\partial \xi_3}
\end{array}\right].$](img115.png) |
|
|
(36) |
If the subsurface offset axes were generated by anything other than uniform shifting (e.g.
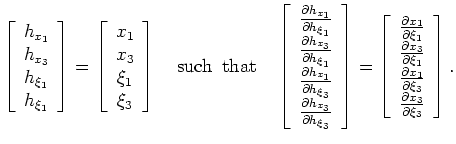 ), then the assumptions behind equations A-11 would not be honored.
), then the assumptions behind equations A-11 would not be honored.
Using these identities in equation A-5 reduces equation A-10 to
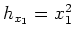 |
(37) |
where the two Jacobian transformations are equivalent (i.e.
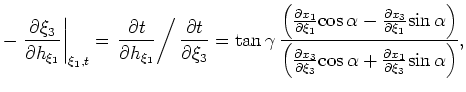 ).
This completes the derivation of equation 10.
).
This completes the derivation of equation 10.
 |
 |
 |
 | Angle-domain common-image gathers in generalized coordinates |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Shragge: Generalized-coordinate ADCIGs
Previous: Acknowledgments
2009-04-13
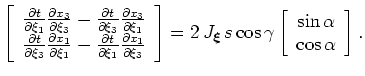 and
and
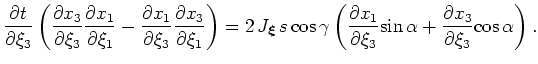
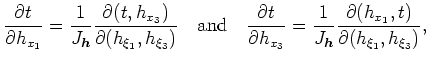 is the subsurface-offset Jacobian of transformation. Expanding the Jacobian notation leads to
is the subsurface-offset Jacobian of transformation. Expanding the Jacobian notation leads to
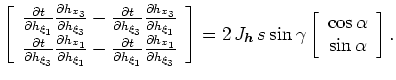 and
and
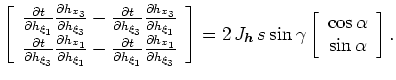 ,
,
![]() ,
,
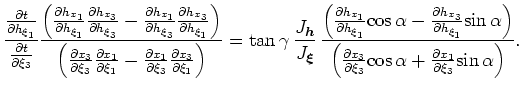 and
and
![]() represent? I assume that the subsurface offset axes are generated by uniform wavefield shifting such that the following equations are valid:
represent? I assume that the subsurface offset axes are generated by uniform wavefield shifting such that the following equations are valid:
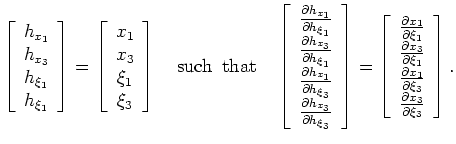 ), then the assumptions behind equations A-11 would not be honored.
), then the assumptions behind equations A-11 would not be honored.
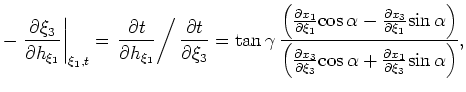 ).
This completes the derivation of equation 10.
).
This completes the derivation of equation 10.