 |
 |
 |
 | Angle-domain common-image gathers in generalized coordinates |  |
![[pdf]](icons/pdf.png) |
Next: Generalized coordinate ADCIGs
Up: ADCIG theory
Previous: Generating subsurface offsets axes
For constant velocity media in conventional Cartesian geometry, a straightforward link exists between differential changes in the travel time, 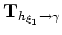 , of rays connecting the source-reflector and reflector-receiver paths to changes in the subsurface offset,
, of rays connecting the source-reflector and reflector-receiver paths to changes in the subsurface offset, 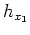 , and depth,
, and depth, 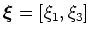 , coordinates. Figure 1a shows the geometry of these variables.
, coordinates. Figure 1a shows the geometry of these variables.
Mathematically, these relationships are
![$\displaystyle \left[ \begin{array}{c}
\frac{\partial t}{\partial h_{x_1}} \fr...
...begin{array}{c}
{\rm sin} \gamma {\rm cos} \gamma
\end{array} \right],$](img43.png) |
|
|
(7) |
where 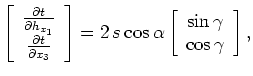 is slowness,
is slowness, 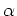 is reflector dip, and
is reflector dip, and 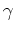 is the reflection opening angle. The right-hand-side of equations 7 are derived by (). Equations 7 can be rewritten as
is the reflection opening angle. The right-hand-side of equations 7 are derived by (). Equations 7 can be rewritten as
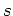 |
(8) |
where the negative sign derives from use of the implicit functions theory (, ). () note that Cartesian ADCIGs become pathogenically degenerate in situations where
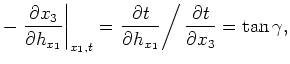 (i.e. for steeply dipping structures where
(i.e. for steeply dipping structures where
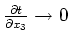 in Figure 1). However, vertically oriented structures are, generally, not well imaged in Cartesian coordinates because of limited steep-angle propagation in downward extrapolation.
in Figure 1). However, vertically oriented structures are, generally, not well imaged in Cartesian coordinates because of limited steep-angle propagation in downward extrapolation.
Finally, because equation 7 has no explicit geometric-dependence, Fourier-based methods can calculate the reflection opening angle directly in the wavenumber domain
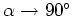 |
(9) |
where
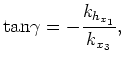 and
and 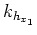 are the wavenumbers in the
are the wavenumbers in the 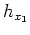 and
and 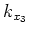 directions, respectively.
directions, respectively.
 |
 |
 |
 | Angle-domain common-image gathers in generalized coordinates |  |
![[pdf]](icons/pdf.png) |
Next: Generalized coordinate ADCIGs
Up: ADCIG theory
Previous: Generating subsurface offsets axes
2009-04-13
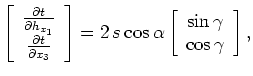 is slowness,
is slowness, 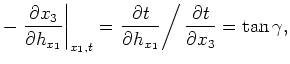 (i.e. for steeply dipping structures where
(i.e. for steeply dipping structures where
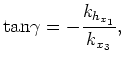 and
and