




Next: Synthetic Data
Up: Vyas: SRMP
Previous: Introduction
A multiple event can be modeled or predicted by convolution of two primary traces. Only surface-related multiples (multiples that reflect at the surface) can be estimated by such a prediction scheme. Understanding the assumption of convolving raw traces with themselves rather than with the primaries, multiple prediction (SRMP) can be written in the Fourier domain Berkhout and Verschuur (1997) as
| 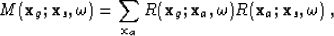 |
(1) |
where R is the data-space volume of shot-gathers defined at geophone (xg)
and source (xs) locations on the acquisition surface. M is the multiple model and 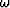 is the frequency. Equation 1 is a
trace-by-trace operation to produce the multiple prediction with any
geophone-source combination. Artman and Matson (2006) showed that equation 1 can be re-written in terms of wavefields (
is the frequency. Equation 1 is a
trace-by-trace operation to produce the multiple prediction with any
geophone-source combination. Artman and Matson (2006) showed that equation 1 can be re-written in terms of wavefields ( 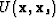 ) as
) as
| 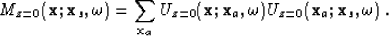 |
(2) |
With a little bit of algebra and the use of reciprocity, Artman and Matson (2006) also showed that equation 2 reduces to
| 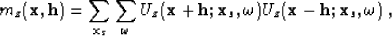 |
(3) |
where mz is the multiple model in image space defined at the image coordinates, surface location x and offset h. A direct analogy can be drawn between equation 3 and the imaging condition for shot-profile migration, the difference being that the shot wavefield is now replaced by the receiver wavefield.
Using the scheme proposed above, multiple prediction can be carried out in the image space, which is theoretically equivalent to doing SRMP in the data space, followed by migration. In this article, I use both the image-space SRMP and data-space SRMP to generate multiple models.





Next: Synthetic Data
Up: Vyas: SRMP
Previous: Introduction
Stanford Exploration Project
5/6/2007