Introduction

Removing multiples from seismic data is essential to producing interpretable subsurface images. Multiples can be categorized on the basis of kinematics and the mechanism of generation. Multiples can be of different types, including specularly reflected or diffracted multiples, peg-leg multiples, surface-related multiples or inter-bed multiples. Strong surface related multiples associated with the free surface are common in marine surveys. With the increase in marine acquisition, surface-related multiples have received more attention, and techniques for handling and removing these multiples have improved.

Kinematics of surface-related multiples can be predicted by auto-convolution of recorded data Anstey and Newman (1966). However, due to discrepancies between modeled and observed multiples in terms of their amplitudes and frequency content, direct subtraction is not possible. Various iterative and adaptive subtraction schemes have been proposed in the past to address this issue. The problem of multiple removal can also be attacked in image space instead of in the data domain Alvarez et al. (2004); Sava and Guitton (2003, 2005). There are some intuitive reasons to prefer image-space prediction over data-space modeling. First, the image space is much smaller than the data space, and hence there are associated computational savings. Second, if we assume perfect knowledge of the velocity, discriminating between multiples and primaries with the help of common-image-point gathers (offset and angle) is fairly straightforward.

Artman and Matson (2006) extended the SRMP approach through commutability of wavefield extrapolation and convolution to predict multiples in image space during shot-profile migration. The image-space SRMP algorithm is computationally cheaper than first carrying out SRMP in the data space and then migrating the data and the multiple model independently to the image space. However, since SRMP is based on convolving recorded data with itself, it yields perfect multiple prediction only when we record all the primary paths that lead to multiple generation. This is true when either our recording geometry is infinite or the subsurface structure is flat. In practice, neither of the aforesaid conditions are likely; in addition, there are situations when the primary escapes the recording geometry, but the corresponding multiple, after hitting a steeply dipping reflector bounces back in and gets recorded. Figure shows the ray path for one such possibility. It is not possible to predict this multiple using SRMP, because we do not record the contributing primaries.

 

raypath Figure 1 A ray path illustrating the situation where the primary escapes the recording geometry but the multiple bounces back and gets recorded.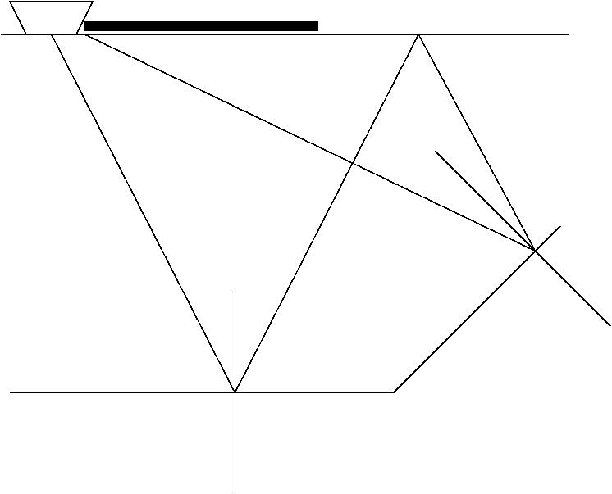

It is difficult to model such multiples; however, image space gives us a better chance to handle them. We can make use of the redundancy present in the image space to address this problem. Multiple events in the data space migrate to a single point in image space (if perfect multiple velocity) but with different opening angles, and a missing event in data space translates to a missing angle in image space. If we can spread the information consistently from one opening angle to another, we may be able to reconstruct the missing part of the multiple model. When the migration velocity is perfect, events in the image space will appear flat in the angle domain, and we can easily infill the missing angles to reconstruct the multiple model. But in general, multiples have very different velocities than the primaries recorded at similar times and show curvature in the angle domain when migrated with the true velocity. The task of infilling is thus not as straightforward as it is for flat gathers. There are two ways to approach this: either we can migrate with the multiple velocity, do infilling and then demigrate, or alternatively, we can use Radon-style transforms to infill gathers with curvature.

In this article I first demonstrate the problem using a simple synthetic example and then illustrate a possible corrective approach. I give a second example using the Sigsbee model, which is a more realistic case.