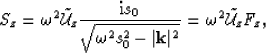Next: Relationship to Pratt's approach
Up: Shragge: TWVA
Previous: Introducing velocity perturbations
The goal of waveform inversion is to invert for the optimal set of
velocity perturbations that minimize the difference between
forward-modeled waveforms and acquired data. The first step in setting
up the inverse problem is defining data residuals, 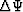 ,
,
| 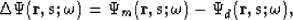 |
(18) |
where 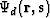 is the recorded data. The L2 residual norm
is used to set up an objective function,
is the recorded data. The L2 residual norm
is used to set up an objective function,
| 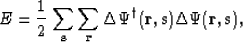 |
(19) |
that is minimized with respect to slowness perturbations 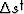
| 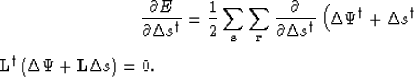 |
(20) |
This results in the following least-squares estimate of the slowness
perturbations
| 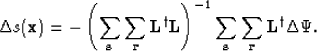 |
(21) |
From here on, the sum over all sources and receivers is implicitly
assumed. Also, we discuss only the gradient vector and the filtering
of the gradient by the inverse Hessian matrix 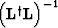 is implicitly assumed.
is implicitly assumed.
The adjoint gradient operator  is a composite matrix
consisting of a number of chained operators (from
equation 16):
is a composite matrix
consisting of a number of chained operators (from
equation 16):
| 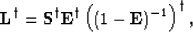 |
(22) |
where scattering operator or at each extrapolation interval, Sz
is defined by (see Appendix A),
| 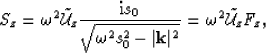 |
(23) |
where 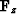 is considered a filter. This allows us to write
composite operator
is considered a filter. This allows us to write
composite operator  with scattering
with scattering 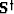 and
filter
and
filter 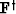 matrices as,
matrices as,
| 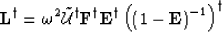 |
(24) |
Inserting this expression into equation 22 yields,
| 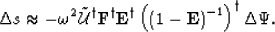 |
(25) |
Thus, using the relationship in equations 6 and
7, leads to the following result,
| 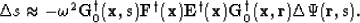 |
(26) |
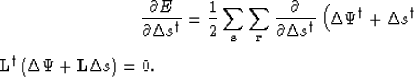
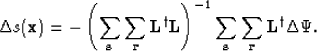
![]() is a composite matrix
consisting of a number of chained operators (from
equation 16):
is a composite matrix
consisting of a number of chained operators (from
equation 16):