Next: Introducing velocity perturbations
Up: Shragge: TWVA
Previous: Introduction
Following Sava and Biondi (2004), I develop equations for imaging by
wavefield extrapolation based on recursive continuation of
the wavefields 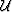 from a given depth level to the next by means of
an extrapolator operator
from a given depth level to the next by means of
an extrapolator operator 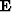
| ![\begin{displaymath}
{\cal U}_{z+\Delta z}= {\mathbf E}_z[{\cal U}_z],\end{displaymath}](img3.gif) |
(1) |
where ![${\mathbf E}_z[]={\rm e}^{{\rm i}k_z \Delta z}$](img4.gif) , kz is
extrapolation wavenumber, and
, kz is
extrapolation wavenumber, and 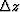 is the depth step.
Throughout this paper, I use a notation where
is the depth step.
Throughout this paper, I use a notation where ![${ \bf A}[x]$](img6.gif) denotes
that operator
denotes
that operator 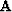 is applied to a field x. Subscripts z and
is applied to a field x. Subscripts z and
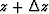 correspond to quantities associated with depth levels z and
correspond to quantities associated with depth levels z and
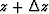 , respectively.
, respectively.
Using this operator notation, a data wavefield 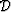 can be recursively
extrapolated through a medium described by model parameters
(i.e. slowness). This operation can be written explicitly in matrix
form,
can be recursively
extrapolated through a medium described by model parameters
(i.e. slowness). This operation can be written explicitly in matrix
form,
| ![\begin{displaymath}
\left[ \begin{array}
{cccccc}
\mathbf{1} & 0 & 0 & ... & 0 &...
...thcal D}_0 \\ 0 \\ 0 \\
\vdots \\
0 \\ \end{array}\right],\end{displaymath}](img10.gif) |
(2) |
where 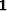 is an identity operator, and fields without subscripts
(e.g.
is an identity operator, and fields without subscripts
(e.g. 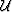 and
and 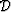 ) refer to complete
wavefields. Equation 2 is written more compactly
as
) refer to complete
wavefields. Equation 2 is written more compactly
as
| 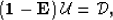 |
(3) |
where 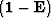 is a Green's function
is a Green's function 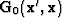 between levels
between levels  and
and 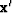 generated by wavefield
extrapolation. The Green's function satisfies the following adjoint
definitions,
generated by wavefield
extrapolation. The Green's function satisfies the following adjoint
definitions,
| 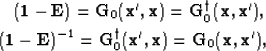 |
(4) |
| (5) |
where superscripts -1 and 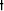 indicate the inverse and adjoint
operation (i.e. complex transpose), respectively.
indicate the inverse and adjoint
operation (i.e. complex transpose), respectively.
Source wavefields well-modeled by a delta function exhibit the following relationships,
| 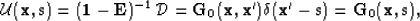 |
(6) |
where 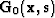 describes the propagation from source point
describes the propagation from source point  throughout the domain denoted by
throughout the domain denoted by  . Note that the choice of
. Note that the choice of
 is arbitrary and an equivalent development applies for a
receiver Green's function
is arbitrary and an equivalent development applies for a
receiver Green's function 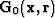 ,
,
| 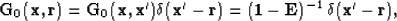 |
(7) |
where  is receiver location.
is receiver location.
![]() can be recursively
extrapolated through a medium described by model parameters
(i.e. slowness). This operation can be written explicitly in matrix
form,
can be recursively
extrapolated through a medium described by model parameters
(i.e. slowness). This operation can be written explicitly in matrix
form,
![\begin{displaymath}
\left[ \begin{array}
{cccccc}
\mathbf{1} & 0 & 0 & ... & 0 &...
...thcal D}_0 \\ 0 \\ 0 \\
\vdots \\
0 \\ \end{array}\right],\end{displaymath}](img10.gif)