




Next: Waveform Inversion Problem
Up: WEMVA Forward Modeling
Previous: WEMVA Forward Modeling
If a velocity perturbation is applied at some depth level, a
perturbed wavefield 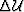 can be derived from the background wavefield
by application of the chain rule to equation 1,
can be derived from the background wavefield
by application of the chain rule to equation 1,
| ![\begin{displaymath}
\Delta {\mathcal U}_{z+\Delta z}= {\mathbf E}_z[\Delta {\mathcal U}_z]+\Delta {\mathcal V}_{z+\Delta z},\end{displaymath}](img26.gif) |
(8) |
where 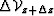 represents the scattered wavefield generated at
represents the scattered wavefield generated at 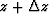 by the interaction of the velocity model at depth z. Field
by the interaction of the velocity model at depth z. Field 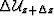 is the accumulated wavefield perturbation corresponding to the
slowness perturbations at all levels above. It is computed by
extrapolating the wavefield perturbations from the level above
is the accumulated wavefield perturbation corresponding to the
slowness perturbations at all levels above. It is computed by
extrapolating the wavefield perturbations from the level above 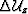 ,plus the scattered wavefield at this level,
,plus the scattered wavefield at this level, 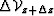 .
.
Equation 8 is also a recursive equation that can be
written in matrix form
| ![\begin{eqnarray}
\left[ \begin{array}
{cccccc}
\mathbf{1} & 0 & 0 & ... & 0 & 0 ...
...{\mathcal U}_2 \\ \vdots \\ {\mathcal U}_n\end{array}\right], & \,\end{eqnarray}](img30.gif) |
(9) |
| (10) |
or in more compact notation as,
| 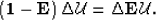 |
(11) |
Operator 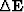 denotes a perturbation of the extrapolation
operator
denotes a perturbation of the extrapolation
operator 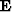 , while quantity
, while quantity 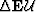 represents a
scattered wavefield and is a function of the medium perturbation given
by the scattering relationship derived in Appendix A. For single
scattering we write,
represents a
scattered wavefield and is a function of the medium perturbation given
by the scattering relationship derived in Appendix A. For single
scattering we write,
| ![\begin{displaymath}
\Delta {\mathcal V}_{z+\Delta z}\equiv \Delta {\mathbf E}_z[...
...athbf E}_z[ {\mathbf S}_z( \tilde{\mathcal U}_z) [ \Delta s] ],\end{displaymath}](img34.gif) |
(12) |
where 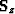 is the scattering operator, and
is the scattering operator, and 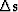 is slowness
perturbation. This expression yields a recursive relationship that
can be written in matrix form:
is slowness
perturbation. This expression yields a recursive relationship that
can be written in matrix form:
| ![\begin{displaymath}
\left[ \begin{array}
{cccccc}
0 & 0 & 0 & ... & 0 & 0\\ {\ma...
...a s_1 \\ \Delta s_2 \\ \vdots \\ \Delta s_n\end{array}\right] ,\end{displaymath}](img38.gif) |
(13) |
or in more compact notation
| 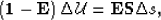 |
(14) |
where vector 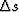 denotes slowness perturbations at all depths.
denotes slowness perturbations at all depths.
Finally, introducing
| 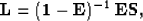 |
(15) |
we can write a simple relationship between slowness 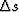 and
wavefield
and
wavefield 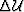 perturbations:
perturbations:
| 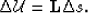 |
(16) |
This expression represents the wavefield scattering caused by the
interaction of the background wavefield with the a medium
perturbation. The total modeled field 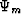 is defined as,
is defined as,
| 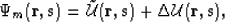 |
(17) |
where 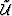 is the background wavefield modeled by
equation 3.
is the background wavefield modeled by
equation 3.





Next: Waveform Inversion Problem
Up: WEMVA Forward Modeling
Previous: WEMVA Forward Modeling
Stanford Exploration Project
5/6/2007
![\begin{eqnarray}
\left[ \begin{array}
{cccccc}
\mathbf{1} & 0 & 0 & ... & 0 & 0 ...
...{\mathcal U}_2 \\ \vdots \\ {\mathcal U}_n\end{array}\right], & \,\end{eqnarray}](img30.gif)
![\begin{displaymath}
\left[ \begin{array}
{cccccc}
\mathbf{1} & 0 & 0 & ... & 0 &...
...\ \vdots \\ \Delta {\mathcal U}_n\end{array}\right] = \nonumber\end{displaymath}](img37.gif)
![\begin{displaymath}
\left[ \begin{array}
{cccccc}
0 & 0 & 0 & ... & 0 & 0\\ {\ma...
...a s_1 \\ \Delta s_2 \\ \vdots \\ \Delta s_n\end{array}\right] ,\end{displaymath}](img38.gif)