




Next: Sigsbee 2b synthetic examples
Up: Image-space SRMP
Previous: Deconvolution
In 1D, let a trace be represented in the Fourier domain by the
expression
| 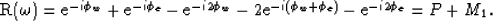 |
(18) |
The trace has primary reflections, P, at phase delays, 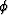 ,
representing a water-bottom and a subsurface event. Also included are
first order multiples, M1, which are the water-bottom multiple at
,
representing a water-bottom and a subsurface event. Also included are
first order multiples, M1, which are the water-bottom multiple at
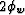 , two peg-leg multiples at
, two peg-leg multiples at 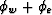 , and the
event multiple at
, and the
event multiple at 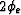 . SRMP dictates the autoconvolution of
P to derive M1, which is clearly true. Including the events
M1 in the autoconvolution will derive the second order multiples as
well.
. SRMP dictates the autoconvolution of
P to derive M1, which is clearly true. Including the events
M1 in the autoconvolution will derive the second order multiples as
well.
Extrapolating trace R to a deeper depth applies a common phase
shift, say 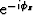 , to all terms in equation 18.
The trace then becomes
, to all terms in equation 18.
The trace then becomes
| 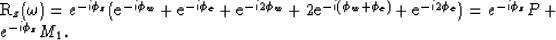 |
(19) |
This equation shows that the extrapolation of data without multiple
subtraction produces the superposition of the redatumed primaries and
the redatumed multiples. The extraction of the zero-time lag in the imaging
condition of migration states that energy in the wavefield should be
mapped into the image domain only when the extrapolation phasor
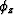 , is equal to the time delay of the event in the data. Thus
the water bottom primary is imaged when
, is equal to the time delay of the event in the data. Thus
the water bottom primary is imaged when 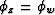 , the water-bottom
multiple is imaged when
, the water-bottom
multiple is imaged when 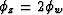 , etc. Whether the data R is
first separated into its constituent parts, P and Mi, or not, it
can be seen where in the image domain the various events in the above
example will be placed.
, etc. Whether the data R is
first separated into its constituent parts, P and Mi, or not, it
can be seen where in the image domain the various events in the above
example will be placed.
However, by first squaring the trace, as dictated by the multiple prediction
imaging condition (equation 9), the water-bottom primary is
mapped into the image domain when 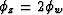 . This is the same
phasor that maps the recorded water-bottom multiple into the image
domain using the conventional imaging condition. Thus, the multiple
prediction in the image space can be directly calculated with a
multiple-only imaging condition due to the commutability of
convolution and extrapolation.
. This is the same
phasor that maps the recorded water-bottom multiple into the image
domain using the conventional imaging condition. Thus, the multiple
prediction in the image space can be directly calculated with a
multiple-only imaging condition due to the commutability of
convolution and extrapolation.
For prestack data in higher dimensions, the phasor 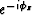 is
the combination of the down-going energy D and the exponential delay
operators in equations 1 and 2.
is
the combination of the down-going energy D and the exponential delay
operators in equations 1 and 2.





Next: Sigsbee 2b synthetic examples
Up: Image-space SRMP
Previous: Deconvolution
Stanford Exploration Project
1/16/2007
![]() , to all terms in equation 18.
The trace then becomes
, to all terms in equation 18.
The trace then becomes
![]() . This is the same
phasor that maps the recorded water-bottom multiple into the image
domain using the conventional imaging condition. Thus, the multiple
prediction in the image space can be directly calculated with a
multiple-only imaging condition due to the commutability of
convolution and extrapolation.
. This is the same
phasor that maps the recorded water-bottom multiple into the image
domain using the conventional imaging condition. Thus, the multiple
prediction in the image space can be directly calculated with a
multiple-only imaging condition due to the commutability of
convolution and extrapolation.
![]() is
the combination of the down-going energy D and the exponential delay
operators in equations 1 and 2.
is
the combination of the down-going energy D and the exponential delay
operators in equations 1 and 2.