Gaussian Pyramid Generation

The Gaussian pyramid generation is done by starting with an initial image 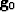$\bold g_0$ and then lowpass filtering this image to obtain a "reduced" image $\bold g_1$. The image is "reduced" in the sense that both spatial density and resolution are decreased. This operation can be continued to obtain a set of images $\bold {\{g_0,g_1,g_2,\ldots g_n\}}$ that form the pyramid image structure. The low pass filtering is done by a procedure equivalent to convolution by a set of local symmetric weighting functions (for example a Gaussian distribution). A fast algorithm for generating such a Gaussian pyramid structure is outlined in the next subsection. Along with the Gaussian pyramid generation, there is also an approximate reverse process of the pyramid generation that tries to expand a reduced image to its original scale. The same algorithm that is used to form the pyramid can also be used to perform the expansion operation as outlined in the following subsection.
 

• Gaussian pyramid generation
• Pyramid expansion
• Mathematical basis of Pyramid Generation
• Laplacian Pyramid