Laplacian Pyramid

The Laplacian pyramid Burt and Adelson (1983) is a sequence of error images 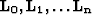$\bold {L_0, L_1, \ldots L_n}$ such that each error image is the difference between two levels of the Gaussian pyramid, that is:

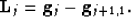$$\bold L_j = \bold g_j - \bold g_{j+1,1}.$$ (7)

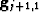where $\bold g_{j+1,1}$ is the image at pyramid level j+1 expanded to size of the image at level j. Thus it is immediately clear tht the Gaussian pyramid formation and expansion process is exact, in the sense that the original image 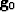$\bold g_0$ is fully recoverable, as :

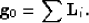$$\bold g_0 = \sum \bold L_i .$$ (8)

The way to do this is to first expand the top pyramid level, 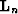$\bold L_n$, and then add the expanded version to L_n-1 to form 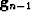$\bold g_{n-1}$. This process is repeated for each level until we reach the base of the pyramid where the original image is fully recovered. Since the top of the pyramid does not have an error image we can treat the image at the top of the pyramid as the error image $\bold L_n$ :

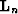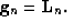$$\bold g_n = \bold L_n .$$ (9)

Notice that the value of each node of the Laplacian pyramid is the difference between the convolutions of two equivalent weighting functions h_l and h_l+1. This operation is similar to convolving the image with an appropriately scaled Laplacian weighting function and hence the name Laplacian pyramid. But the cost involved with this operation would be substantially more than constructing error images as a difference between two pyramid levels. The Laplacian pyramid can be treated as a set of band-pass filtered versions of the original image just as the Gaussian pyramid represents low-pass filtered versions of the original image. In the next section I use the concepts of both Gaussian pyramids and Laplacian pyramids and the fact that the pyramid forming process is exactly reversible to show how interpolation of missing data can be done using the pyramid scheme.