Having generalized to dipping angles the analysis of the kinematics of the offset-to-angle transformation, we generalize to dipping reflectors the analysis of the residual moveout in ADCIGs caused by errors in anisotropic velocity parameters. As in Biondi (2005a), we derive the RMO function by linearizing the relationship of the imaging depth in the angle domain with respect to perturbations in the anisotropic parameters. The linearization is evaluated around the correct migration velocity function; that is, when the image in the subsurface-offset domain is well focused at zero offset. We derive relationships under the assumption that the velocity perturbations are limited to a homogeneous half-space above the reflector.
We use a notation that is the same as in Biondi (2005a): the
VTI velocity function is described by the vector
![]() , where VV is the velocity of a vertical ray, VH
is the velocity of a horizontal ray and VN is the NMO velocity.
The perturbations are defined as the combination of one multiplicative factor
for each of the velocities (
, where VV is the velocity of a vertical ray, VH
is the velocity of a horizontal ray and VN is the NMO velocity.
The perturbations are defined as the combination of one multiplicative factor
for each of the velocities (![]() ) and one multiplicative factor for all
velocities (
) and one multiplicative factor for all
velocities (![]() ,
,![]() and
and ![]() ): the perturbed
velocity
): the perturbed
velocity ![]() is defined as:
is defined as:
| (18) |
In the case of dipping reflectors, the equation for
the differentiation of the image
point depth in the angle domain ![]() with respect to the i-th
component in the perturbation vector can be written:
with respect to the i-th
component in the perturbation vector can be written:
| |
(19) |
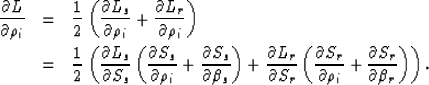 |
||
| (20) |
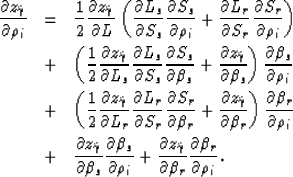 |
||
| (21) |