RMO function with uniform scaling of velocity

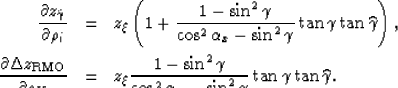
In case of uniform scaling of velocity, the derivative of the slowness with respect to a uniform scaling of the velocity has a simple form:

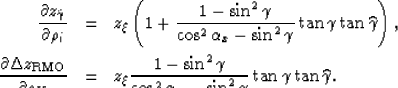$$\begin{eqnarray} \frac{\partial S \left(x \right)}{\partial \rho_V} =-S\left(x\right).\end{eqnarray}$$ (28)

The derivatives of the imaging depth $z_{\tilde{\gamma}}$ and of the residual moveout with respect to the perturbation component $\rho_V$ have the following forms (refer to equations (53) and (55)):

$$\begin{eqnarray} \frac{\partial z_{\tilde{\gamma}}}{\partial \rho_{i}} &=& z_\xi... ...a}{\cos^2\alpha_x-\sin^2\gamma} \tan \gamma \tan \widehat{\gamma}.\end{eqnarray}$$ (29) (30)

The dependence of equation (30) on the group angles increases the complexity of its use. However, we showed in the preceding section that it is possible to compute the angle $\gamma$ from $\widehat{\gamma}$. We first compute $\tilde{\gamma}$ from $\widehat{\gamma}$ by solving a system of two quadratic equations (equations (15) and (16)) then computes $\gamma$ from $\tilde{\gamma}$by using equation (17). The computational cost of evaluating the group angles is negligible and it is important to introduce the distinction between the ``three aperture angles'': $\gamma$, $\tilde{\gamma}$ and $\widehat{\gamma}$.

Equations (30) and (29) are consistent with the ones derived in the isotropic case with dipping reflectors Biondi and Symes (2003). Under the assumption that the medium is isotropic, $\widehat{\gamma}=\gamma$ and the derivatives of the imaging depth $z_{\tilde{\gamma}}$ and of the residual moveout with respect to the perturbation component $\rho_V$ are

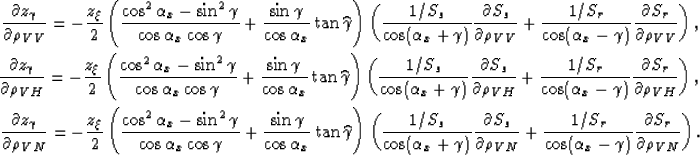$$\begin{eqnarray} \left. \frac{\partial z_{\tilde{\gamma}}}{\partial \rho_{i}} \r... ...{iso}} &=& z_\xi \frac{\sin^2\gamma}{\cos^2\alpha_x-\sin^2\gamma}.\end{eqnarray}$$ (31) (32)